![P\in \Bbb{R}[x] P\in \Bbb{R}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/9927706e87edbb5cb5ed1f7b235a8bb5.png) τέτοια ώστε
τέτοια ώστε 
Συντονιστές: achilleas, emouroukos, silouan
 με πραγματικούς συντελεστές, τα ακόλουθα είναι ισοδύναμα:
με πραγματικούς συντελεστές, τα ακόλουθα είναι ισοδύναμα: 
![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right).} \displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right).}](/forum/ext/geomar/texintegr/latexrender/pictures/8daeead15c603371aea55c412916220c.png)
 Το
Το  είναι το μηδενικό πολυώνυμο, ή υπάρχει φυσικός αριθμός
είναι το μηδενικό πολυώνυμο, ή υπάρχει φυσικός αριθμός  τέτοιος, ώστε
τέτοιος, ώστε 
![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right)} \displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/409b1cbc0e722247d8361e5081dbe52a.png) και ότι το
και ότι το  δεν είναι το μηδενικό πολυώνυμο. Τότε, θα υπάρχουν πραγματικοί αριθμοί
δεν είναι το μηδενικό πολυώνυμο. Τότε, θα υπάρχουν πραγματικοί αριθμοί 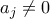 και φυσικοί αριθμοί
και φυσικοί αριθμοί  ,
, , με
, με  ώστε
ώστε  Έχουμε τότε ότι:
Έχουμε τότε ότι:![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} - Q\left( {{x^2}} \right) = \sum\limits_{j = 1}^m {\left( {a_j^2 - {a_j}} \right){x^{2{k_j}}}} + \sum\limits_{1 \le i < j \le m} {2{a_i}{a_j}{x^{{k_i} + {k_j}}}} } \displaystyle{{\left[ {Q\left( x \right)} \right]^2} - Q\left( {{x^2}} \right) = \sum\limits_{j = 1}^m {\left( {a_j^2 - {a_j}} \right){x^{2{k_j}}}} + \sum\limits_{1 \le i < j \le m} {2{a_i}{a_j}{x^{{k_i} + {k_j}}}} }](/forum/ext/geomar/texintegr/latexrender/pictures/78beb5d490d32aa370655509f8d0720c.png)

 , τότε ο συντελεστής του
, τότε ο συντελεστής του  στην
στην  είναι ίσος με
είναι ίσος με  πράγμα άτοπο. Επομένως,
πράγμα άτοπο. Επομένως, 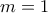 και
και  Αλλά από τη σχέση
Αλλά από τη σχέση ![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right)} \displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/409b1cbc0e722247d8361e5081dbe52a.png) προκύπτει ότι
προκύπτει ότι  , οπότε
, οπότε  και ο Ισχυρισμός έπεται.
και ο Ισχυρισμός έπεται.![\displaystyle{P\left( {{x^2}} \right) + x\left[ {3P\left( x \right) + P\left( { - x} \right)} \right] = {\left[ {P\left( x \right)} \right]^2} + 2{x^2}} \displaystyle{P\left( {{x^2}} \right) + x\left[ {3P\left( x \right) + P\left( { - x} \right)} \right] = {\left[ {P\left( x \right)} \right]^2} + 2{x^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/72409e17adcd060848f0ea99acc25c17.png)

 στη θέση του
στη θέση του  , οπότε προκύπτει ότι:
, οπότε προκύπτει ότι:![\displaystyle{P\left( {{x^2}} \right) - x\left[ {3P\left( { - x} \right) + P\left( x \right)} \right] = {\left[ {P\left( { - x} \right)} \right]^2} + 2{x^2}} \displaystyle{P\left( {{x^2}} \right) - x\left[ {3P\left( { - x} \right) + P\left( x \right)} \right] = {\left[ {P\left( { - x} \right)} \right]^2} + 2{x^2}}](/forum/ext/geomar/texintegr/latexrender/pictures/6b91cb00b52c0cd6182afed0edc05fce.png)
 .
. και
και  κατά μέλη προκύπτει ότι:
κατά μέλη προκύπτει ότι:![\displaystyle{4x\left[ {P\left( x \right) + P\left( { - x} \right)} \right] = {\left[ {P\left( x \right)} \right]^2} - {\left[ {P\left( { - x} \right)} \right]^2} \Leftrightarrow } \displaystyle{4x\left[ {P\left( x \right) + P\left( { - x} \right)} \right] = {\left[ {P\left( x \right)} \right]^2} - {\left[ {P\left( { - x} \right)} \right]^2} \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/b1912f5dbac2a7c84df3c27f5ab3051d.png)
![\displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.} \displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.}](/forum/ext/geomar/texintegr/latexrender/pictures/582da8132c1846a5bb0b74d78a1957ef.png)

 δηλαδή
δηλαδή 
 βρίσκουμε ότι
βρίσκουμε ότι![\displaystyle{P\left( {{x^2}} \right) + 2xP\left( x \right) = {\left[ {P\left( x \right)} \right]^2} + 2{x^2} \Leftrightarrow } \displaystyle{P\left( {{x^2}} \right) + 2xP\left( x \right) = {\left[ {P\left( x \right)} \right]^2} + 2{x^2} \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/8d62a509dabf26a286b16737c7f78415.png)
![\displaystyle{ \Leftrightarrow {\left[ {P\left( x \right) - x} \right]^2} = P\left( {{x^2}} \right) - {x^2}.} \displaystyle{ \Leftrightarrow {\left[ {P\left( x \right) - x} \right]^2} = P\left( {{x^2}} \right) - {x^2}.}](/forum/ext/geomar/texintegr/latexrender/pictures/a7770b5abfe2b3523227580bac421ebf.png)
 ισχύει
ισχύει ![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right),} \displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right),}](/forum/ext/geomar/texintegr/latexrender/pictures/1e58cc7fe943297f6ab50d205ad21af3.png) οπότε από τον Ισχυρισμό έχουμε ότι
οπότε από τον Ισχυρισμό έχουμε ότι  ή
ή  για κάποιο φυσικό αριθμό
για κάποιο φυσικό αριθμό  . Επειδή, όμως, ισχύει
. Επειδή, όμως, ισχύει  ο
ο  θα είναι περιττός. Προκύπτει, λοιπόν, ότι
θα είναι περιττός. Προκύπτει, λοιπόν, ότι 

 φυσικός αριθμός.
φυσικός αριθμός.
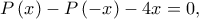 δηλαδή
δηλαδή 
 βρίσκουμε ότι
βρίσκουμε ότι![\displaystyle{P\left( {{x^2}} \right) + 4xP\left( x \right) - 4{x^2} = {\left[ {P\left( x \right)} \right]^2} + 2{x^2} \Leftrightarrow } \displaystyle{P\left( {{x^2}} \right) + 4xP\left( x \right) - 4{x^2} = {\left[ {P\left( x \right)} \right]^2} + 2{x^2} \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/b07f56821fb4161ad17aba87ab8d9747.png)
![\displaystyle{ \Leftrightarrow {\left[ {P\left( x \right) - 2x} \right]^2} = P\left( {{x^2}} \right) - 2x^2.} \displaystyle{ \Leftrightarrow {\left[ {P\left( x \right) - 2x} \right]^2} = P\left( {{x^2}} \right) - 2x^2.}](/forum/ext/geomar/texintegr/latexrender/pictures/6429faadd06b11e0358cb87952d0fa39.png)
 ισχύει
ισχύει ![\displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right),} \displaystyle{{\left[ {Q\left( x \right)} \right]^2} = Q\left( {{x^2}} \right),}](/forum/ext/geomar/texintegr/latexrender/pictures/1e58cc7fe943297f6ab50d205ad21af3.png) οπότε από τον Ισχυρισμό έχουμε ότι
οπότε από τον Ισχυρισμό έχουμε ότι  ή
ή  για κάποιο φυσικό αριθμό
για κάποιο φυσικό αριθμό  . Επειδή, όμως, ισχύει
. Επειδή, όμως, ισχύει  ο
ο  θα είναι άρτιος. Προκύπτει, λοιπόν, ότι
θα είναι άρτιος. Προκύπτει, λοιπόν, ότι

 φυσικός αριθμός.
φυσικός αριθμός. .
. ήταν λανθασμένη.
ήταν λανθασμένη.Στην σχέση που είναι τα ερωτηματικά, μπορεί κάποιος να εξηγήσει γιατί αναγκαστικάemouroukos έγραψε: ↑Τρί Μάιος 01, 2012 8:38 am
![\displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.} \displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.}](/forum/ext/geomar/texintegr/latexrender/pictures/582da8132c1846a5bb0b74d78a1957ef.png)



Διακρίνουμε τώρα δύο περιπτώσεις:

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι περιττός. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι άρτιος. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.
Εύκολα επαληθεύουμε ότι τα παραπάνω πολυώνυμα επαληθεύουν τη δοσμένη σχέση.
 για κάθε
για κάθε  ή
ή  για κάθε
για κάθε  ; (ενώ είναι γνωστό ότι δεν ισχύει κάτι τέτοιο στις συναρτήσεις)
; (ενώ είναι γνωστό ότι δεν ισχύει κάτι τέτοιο στις συναρτήσεις)Ορέστης Λιγνός έγραψε: ↑Πέμ Δεκ 20, 2018 11:25 amΣτην σχέση που είναι τα ερωτηματικά, μπορεί κάποιος να εξηγήσει γιατί αναγκαστικάemouroukos έγραψε: ↑Τρί Μάιος 01, 2012 8:38 am
![\displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.} \displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.}](/forum/ext/geomar/texintegr/latexrender/pictures/582da8132c1846a5bb0b74d78a1957ef.png)



Διακρίνουμε τώρα δύο περιπτώσεις:

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι περιττός. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι άρτιος. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.
Εύκολα επαληθεύουμε ότι τα παραπάνω πολυώνυμα επαληθεύουν τη δοσμένη σχέση.
για κάθε
ή
για κάθε
; (ενώ είναι γνωστό ότι δεν ισχύει κάτι τέτοιο στις συναρτήσεις)
Ευχαριστώ,
Ορέστης.
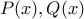 πολυωνυμικές συναρτήσεις με βαθμούς σαν πολυώνυμα
πολυωνυμικές συναρτήσεις με βαθμούς σαν πολυώνυμα  και
και 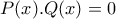 για τουλάχιστον
για τουλάχιστον  διαφορετικά
διαφορετικά 

Ευχαριστώ πολύ Σταύρο. Καλές Γιορτές.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Δεκ 20, 2018 11:45 amΟρέστης Λιγνός έγραψε: ↑Πέμ Δεκ 20, 2018 11:25 amΣτην σχέση που είναι τα ερωτηματικά, μπορεί κάποιος να εξηγήσει γιατί αναγκαστικάemouroukos έγραψε: ↑Τρί Μάιος 01, 2012 8:38 am
![\displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.} \displaystyle{ \Leftrightarrow \left[ {P\left( x \right) + P\left( { - x} \right)} \right]\left[ {P\left( x \right) - P\left( { - x} \right) - 4x} \right] = 0.}](/forum/ext/geomar/texintegr/latexrender/pictures/582da8132c1846a5bb0b74d78a1957ef.png)



Διακρίνουμε τώρα δύο περιπτώσεις:

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι περιττός. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.

δηλαδή
Τότε, με αντικατάσταση στηνβρίσκουμε ότι
Επομένως, για το πολυώνυμοισχύει
οπότε από τον Ισχυρισμό έχουμε ότι
ή
για κάποιο φυσικό αριθμό
. Επειδή, όμως, ισχύει
ο
θα είναι άρτιος. Προκύπτει, λοιπόν, ότι

ή
όπουφυσικός αριθμός.
Εύκολα επαληθεύουμε ότι τα παραπάνω πολυώνυμα επαληθεύουν τη δοσμένη σχέση.
για κάθε
ή
για κάθε
; (ενώ είναι γνωστό ότι δεν ισχύει κάτι τέτοιο στις συναρτήσεις)
Ευχαριστώ,
Ορέστης.
Εδώ έχουμε πολυωνυμικές συναρτήσεις.
Για αυτές ισχύει.
Ανπολυωνυμικές συναρτήσεις με βαθμούς σαν πολυώνυμα
και
για τουλάχιστον
διαφορετικά

τότε ένα τουλάχιστον από τα
Ισχύει.
Δεν νομίζω ότι χρειάζεται απόδειξη.
Αν ζητηθεί ευχαρίστως να την γράψω.
O δακτύλιοςΟρέστης Λιγνός έγραψε: ↑Πέμ Δεκ 20, 2018 11:25 am
Στην σχέση που είναι τα ερωτηματικά, μπορεί κάποιος να εξηγήσει γιατί αναγκαστικάγια κάθε
ή
για κάθε
; (ενώ είναι γνωστό ότι δεν ισχύει κάτι τέτοιο στις συναρτήσεις)
Ευχαριστώ,
Ορέστης.
![R[x] R[x]](/forum/ext/geomar/texintegr/latexrender/pictures/c5b845aa2373916b6d15dbfe5ce5aae3.png) δεν έχει μηδενοδιαιρέτες Ορέστη. Είναι ακέραια περιοχή.
δεν έχει μηδενοδιαιρέτες Ορέστη. Είναι ακέραια περιοχή.Να ξεκαθαρίσω ότι θεωρώ την απόδειξη του Βαγγέλη την πλέον εύστοχη.emouroukos έγραψε: ↑Τρί Μάιος 01, 2012 8:38 amΙσχυρισμός: Για ένα πολυώνυμομε πραγματικούς συντελεστές, τα ακόλουθα είναι ισοδύναμα:

Το
είναι το μηδενικό πολυώνυμο, ή υπάρχει φυσικός αριθμός
τέτοιος, ώστε
 μπορεί να έχει και μιγαδικούς συντελεστές.
μπορεί να έχει και μιγαδικούς συντελεστές. 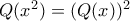 στο
στο 
 στο
στο 
 ισχύει και στο
ισχύει και στο 
 στο
στο 
 είναι ρίζα του
είναι ρίζα του  τότε και
τότε και  είναι
είναι 
 έχει μη μηδενική ρίζα θα άπειρες που
έχει μη μηδενική ρίζα θα άπειρες που 


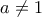 τότε
τότε 


 τότε οι ρίζες του είναι τα
τότε οι ρίζες του είναι τα 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες