
Mη γραμμικό σύστημα
Συντονιστές: achilleas, emouroukos, silouan
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Mη γραμμικό σύστημα
Θέτω :
 και η δεύτερη γίνεται:
και η δεύτερη γίνεται:  .
.Έτσι


αφού λόγω περιοδικότητας οι ρίζες επαναλαμβάνονται.
Τελικά οι ρίζες είναι :
α)
 ή συμμετρικά
ή συμμετρικάβ)
 ή συμμετρικά
ή συμμετρικά γ)
 ή συμμετρικά
ή συμμετρικά- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Mη γραμμικό σύστημα
Ας δούμε και την διαπραγμάτευση που ακολουθεί, μετά από την άριστη λύση του Νίκου και μόνο για λόγους πολυφωνίας.
Επειδή έχουμε το άθροισμα των τετραγώνων αρκεί να προσδιορίσουμε το γινόμενο και αυτό προς χάριν της στόχευσης δημιουργίας ομογενούς συστήματος.
Θέτουμε και διαπιστώνουμε ότι
και διαπιστώνουμε ότι 
άρα έχουμε![\displaystyle{\left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = - \frac{1}{2}} \right] \vee \left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = \frac{1}{4}} \right]} \displaystyle{\left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = - \frac{1}{2}} \right] \vee \left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = \frac{1}{4}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/0f261814219ed12fe06d3ccd053904e8.png) που πλέον επιλύουμε απλά.
που πλέον επιλύουμε απλά.
Επειδή έχουμε το άθροισμα των τετραγώνων αρκεί να προσδιορίσουμε το γινόμενο και αυτό προς χάριν της στόχευσης δημιουργίας ομογενούς συστήματος.
Θέτουμε
 και διαπιστώνουμε ότι
και διαπιστώνουμε ότι 
άρα έχουμε
![\displaystyle{\left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = - \frac{1}{2}} \right] \vee \left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = \frac{1}{4}} \right]} \displaystyle{\left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = - \frac{1}{2}} \right] \vee \left[ {\left( {{x^2} + {y^2} = 1} \right) \wedge xy = \frac{1}{4}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/0f261814219ed12fe06d3ccd053904e8.png) που πλέον επιλύουμε απλά.
που πλέον επιλύουμε απλά.S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Mη γραμμικό σύστημα
και η κλασσική μέθοδος (γιατί ζήλεψα)


Οπότε καταλήγουμε στα συστήματα:
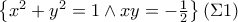
και



Οπότε καταλήγουμε στα συστήματα:
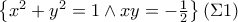
και

Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
