 διαιρείται σε
διαιρείται σε  στοιχειώδη (ίσα) κυβάκια. Χρησιμοποιώντας
στοιχειώδη (ίσα) κυβάκια. Χρησιμοποιώντας  διαφορετικά χρώματα βάφουμε τα στοιχειώδη κυβάκια έτσι ώστε κάθε χρώμα να χρησιμοποιείται ακριβώς
διαφορετικά χρώματα βάφουμε τα στοιχειώδη κυβάκια έτσι ώστε κάθε χρώμα να χρησιμοποιείται ακριβώς  φορές.
φορές.Να δειχθεί ότι σε κάποιο γκρουπ
 συνεχόμενων κύβων (δηλαδή το αντίστοιχο με τις στήλες και τις σειρές σειρές ενός πίνακα δύο διαστάσεων αλλά στις τρεις διαστάσεις) εμφανίζονται τουλάχιστον
συνεχόμενων κύβων (δηλαδή το αντίστοιχο με τις στήλες και τις σειρές σειρές ενός πίνακα δύο διαστάσεων αλλά στις τρεις διαστάσεις) εμφανίζονται τουλάχιστον  διαφορετικά χρώματα.
διαφορετικά χρώματα.
 για το πλήθος των οριζόντιων, κάθετων και εγκάρσιων γραμμών που περιέχουν το χρώμα
για το πλήθος των οριζόντιων, κάθετων και εγκάρσιων γραμμών που περιέχουν το χρώμα  . Έχουμε
. Έχουμε 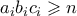 για κάθε
για κάθε ![\displaystyle (a_1 + \cdots + a_{n^2})(b_1+\cdots+b_{n^2})(c_1+\cdots+c_{n^2}) \geqslant (\sqrt[3]{a_1b_1c_1} + \cdots +\sqrt[3]{a_{n^2}b_{n^2}c_{n^2}} )^3 \geqslant n^7 \displaystyle (a_1 + \cdots + a_{n^2})(b_1+\cdots+b_{n^2})(c_1+\cdots+c_{n^2}) \geqslant (\sqrt[3]{a_1b_1c_1} + \cdots +\sqrt[3]{a_{n^2}b_{n^2}c_{n^2}} )^3 \geqslant n^7](/forum/ext/geomar/texintegr/latexrender/pictures/704d56bdf69ab559ae1743f3380e5cc2.png)
 . Άρα σε μια από τις οριζόντιες γραμμές θα εμφανίζονται τουλάχιστον
. Άρα σε μια από τις οριζόντιες γραμμές θα εμφανίζονται τουλάχιστον 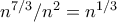 χρώματα.
χρώματα.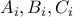 το πλήθος των οριζόντιων, κάθετων και εγκάρσιων λωρίδων
το πλήθος των οριζόντιων, κάθετων και εγκάρσιων λωρίδων  που περιέχουν το χρώμα
που περιέχουν το χρώμα 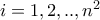 .
. (
( ) ορίζω
) ορίζω  αν το χρώμα
αν το χρώμα  αλλιώς.
αλλιώς. χρώματα.
χρώματα. .
. .
. .
.![\displaystyle E\geq \sum_{i=1}^{n^2}\dfrac{3\sqrt[3]{A_iB_iC_i}}{3n^2}\geq \sum_{i=1}^{n^2}\dfrac{ \sqrt[3]{n}}{n^2}=n^{1/3} \displaystyle E\geq \sum_{i=1}^{n^2}\dfrac{3\sqrt[3]{A_iB_iC_i}}{3n^2}\geq \sum_{i=1}^{n^2}\dfrac{ \sqrt[3]{n}}{n^2}=n^{1/3}](/forum/ext/geomar/texintegr/latexrender/pictures/e708538c94c2f4d7a450384b98249282.png) .
.