 ως τελική απάντηση. Παρατήρησε ότι υπάρχουν πολλοί τρόποι να γράψει την απάντηση ως
ως τελική απάντηση. Παρατήρησε ότι υπάρχουν πολλοί τρόποι να γράψει την απάντηση ως  με
με  θετικούς ακεραίους. Για κάθε τέτοιο τρόπο υπολόγισε το
θετικούς ακεραίους. Για κάθε τέτοιο τρόπο υπολόγισε το 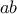 και το έγραψε στην μορφή
και το έγραψε στην μορφή  για κάποιον ρητό
για κάποιον ρητό  .
.Να βρεθεί το άθροισμα όλων των
 .
.Συντονιστές: Demetres, silouan
 ως τελική απάντηση. Παρατήρησε ότι υπάρχουν πολλοί τρόποι να γράψει την απάντηση ως
ως τελική απάντηση. Παρατήρησε ότι υπάρχουν πολλοί τρόποι να γράψει την απάντηση ως  με
με  θετικούς ακεραίους. Για κάθε τέτοιο τρόπο υπολόγισε το
θετικούς ακεραίους. Για κάθε τέτοιο τρόπο υπολόγισε το 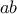 και το έγραψε στην μορφή
και το έγραψε στην μορφή  για κάποιον ρητό
για κάποιον ρητό  .
. .
.Καταρχήν, είναι προφανές ότιDemetres έγραψε: ↑Τετ Νοέμ 28, 2018 9:40 pmΟ Αντρέας έλυσε ένα μαθηματικό πρόβλημα και βρήκεως τελική απάντηση. Παρατήρησε ότι υπάρχουν πολλοί τρόποι να γράψει την απάντηση ως
με
θετικούς ακεραίους. Για κάθε τέτοιο τρόπο υπολόγισε το
και το έγραψε στην μορφή
για κάποιον ρητό
.
Να βρεθεί το άθροισμα όλων των.
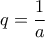 (πράγματι,
(πράγματι,  .
.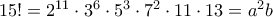 , και άρα
, και άρα 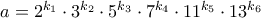 .
. , συνεπώς κάθε
, συνεπώς κάθε  είναι μικρότερο από τον αντίστοιχο εκθέτη στο δεξί μέλος.
είναι μικρότερο από τον αντίστοιχο εκθέτη στο δεξί μέλος. , και επομένως ο
, και επομένως ο  πρέπει να διαιρεί τον
πρέπει να διαιρεί τον  .
. .
. οι διαιρέτες του
οι διαιρέτες του  , και
, και 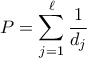 .
. με
με  , οπότε είναι
, οπότε είναι  .
. με
με  πρώτους, είναι
πρώτους, είναι  .
. , και τελικά
, και τελικά 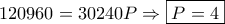 και τελειώσαμε.
και τελειώσαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες