Καλησπέρα,
Έστω
![\left[a_1,b_1\right],\ldots,\left[a_{mn+1},b_{mn+1}\right] \left[a_1,b_1\right],\ldots,\left[a_{mn+1},b_{mn+1}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/caecde268e541290347df5f191a38d9d.png)
τα διαστήματα,όπου

,και έστω ότι δεν ισχύει η δεύτερη συνθήκη.Διατάσουμε τους αριθμούς
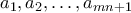
σε αύξουσα σειρά.Η υπόθεσή μας,μας εξασφαλίζει ότι,αν επιλέξουμε δείκτες

,τότε υπάρχει ένας από αυτούς,έστω ο

που είναι τέτοιος ώστε
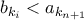
,γιατί διαφορετικά τα διαστήματα
![\left[a_{k_1},b_{k_1}\right],\ldots,\left[a_{k_{n+1}},b_{k_{n+1}}\right] \left[a_{k_1},b_{k_1}\right],\ldots,\left[a_{k_{n+1}},b_{k_{n+1}}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/7773016d67d8ddd1f16a4751f182ca28.png)
θα είχαν μη κενή τομή.Συνεπώς:

Επιλέγουμε τους

και βρίσκουμε ότι υπάρχει
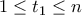
τέτοιος ώστε
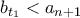
.

Επιλέγουμε τους

και βρίσκουμε ότι υπάρχει
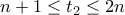
τέτοιος ώστε

.


Επιλέγουμε τους
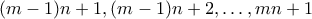
και βρίσκουμε ότι υπάρχει
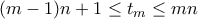
τέτοιος ώστε
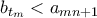
.
Τα διαστήματα
![\left[a_{t_1},b_{t_1}\right],\ldots ,\left[a_{t_m},b_{t_m}\right],\left[a_{mn+1},b_{mn+1}\right] \left[a_{t_1},b_{t_1}\right],\ldots ,\left[a_{t_m},b_{t_m}\right],\left[a_{mn+1},b_{mn+1}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/31055e437a1f3a00775bf4f26f63d33b.png)
είναι ανά δύο ξένα,από όπου έπεται το ζητούμενο.
 . Δίνονται
. Δίνονται  κλειστά διαστήματα στο
κλειστά διαστήματα στο  . Να δειχθεί ότι ισχύει τουλάχιστον ένα από τα πιο κάτω:
. Να δειχθεί ότι ισχύει τουλάχιστον ένα από τα πιο κάτω: από αυτά τα διαστήματα τα οποία είναι ξένα μεταξύ τους.
από αυτά τα διαστήματα τα οποία είναι ξένα μεταξύ τους.  από αυτά τα διαστήματα τα οποία έχουν τουλάχιστον ένα κοινό σημείο τομής.
από αυτά τα διαστήματα τα οποία έχουν τουλάχιστον ένα κοινό σημείο τομής.
![\left[a_1,b_1\right],\ldots,\left[a_{mn+1},b_{mn+1}\right] \left[a_1,b_1\right],\ldots,\left[a_{mn+1},b_{mn+1}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/caecde268e541290347df5f191a38d9d.png) τα διαστήματα,όπου
τα διαστήματα,όπου  ,και έστω ότι δεν ισχύει η δεύτερη συνθήκη.Διατάσουμε τους αριθμούς
,και έστω ότι δεν ισχύει η δεύτερη συνθήκη.Διατάσουμε τους αριθμούς 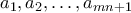 σε αύξουσα σειρά.Η υπόθεσή μας,μας εξασφαλίζει ότι,αν επιλέξουμε δείκτες
σε αύξουσα σειρά.Η υπόθεσή μας,μας εξασφαλίζει ότι,αν επιλέξουμε δείκτες  ,τότε υπάρχει ένας από αυτούς,έστω ο
,τότε υπάρχει ένας από αυτούς,έστω ο  που είναι τέτοιος ώστε
που είναι τέτοιος ώστε 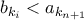 ,γιατί διαφορετικά τα διαστήματα
,γιατί διαφορετικά τα διαστήματα ![\left[a_{k_1},b_{k_1}\right],\ldots,\left[a_{k_{n+1}},b_{k_{n+1}}\right] \left[a_{k_1},b_{k_1}\right],\ldots,\left[a_{k_{n+1}},b_{k_{n+1}}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/7773016d67d8ddd1f16a4751f182ca28.png) θα είχαν μη κενή τομή.Συνεπώς:
θα είχαν μη κενή τομή.Συνεπώς: Επιλέγουμε τους
Επιλέγουμε τους  και βρίσκουμε ότι υπάρχει
και βρίσκουμε ότι υπάρχει 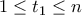 τέτοιος ώστε
τέτοιος ώστε 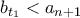 .
. και βρίσκουμε ότι υπάρχει
και βρίσκουμε ότι υπάρχει 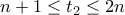 τέτοιος ώστε
τέτοιος ώστε  .
.
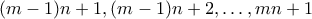 και βρίσκουμε ότι υπάρχει
και βρίσκουμε ότι υπάρχει 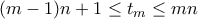 τέτοιος ώστε
τέτοιος ώστε 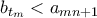 .
.![\left[a_{t_1},b_{t_1}\right],\ldots ,\left[a_{t_m},b_{t_m}\right],\left[a_{mn+1},b_{mn+1}\right] \left[a_{t_1},b_{t_1}\right],\ldots ,\left[a_{t_m},b_{t_m}\right],\left[a_{mn+1},b_{mn+1}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/31055e437a1f3a00775bf4f26f63d33b.png) είναι ανά δύο ξένα,από όπου έπεται το ζητούμενο.
είναι ανά δύο ξένα,από όπου έπεται το ζητούμενο.![I = [a,b] I = [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/bfcd0aa502a23a6e5eb8fdf7513d2ae3.png) είναι μικρότερο του διαστήματος
είναι μικρότερο του διαστήματος ![J = [c,d] J = [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/dc2200eba6d9891b2286dafdcc23ffa0.png) (όπου
(όπου  και
και 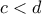 ) αν
) αν  .)
.)