Demetres έγραψε:Σε μια

σκακιέρα είναι τοποθετημένοι

πύργοι ώστε να μην απειλούνται μεταξύ τους.
Κάθε ένας από αυτούς τους πύργους κάνει μία κίνηση όπως ένας ίππος. Να δειχθεί ότι μετά από αυτό υπάρχουν δυο πύργοι που απειλούνται μεταξύ τους. (Ή που βρίσκονται στην ίδια θέση.)
Η λύση αυτή αντικαθιστά μια προηγούμενη που όμως ήταν εσφαλμένη. Ευχαριστώ τον Δημήτρη Χριστοφίδη για την υπόδειξη του σφάλματος.
Θεωρούμε τα τετραγωνάκια της σκακιέρας αριθμημένα σαν να ήταν Καρτεσιανό επίπεδο, αρχίζοντας από το κάτω αριστερά το οποίο είναι το

μέχρι το πάνω δεξιά

. Αν θεωρήσουμε ότι το

είναι μαύρο, τότε τα υπόλοιπα μαύρα είναι ακριβώς τα

με

άρτιος.
Έστω ότι αρχική διάταξη των πύργων είναι στις θέσεις

. Αφού οι πύργοι δεν απειλούνται, σημαίνει ότι οι αριθμοί

είναι αναδιάταξη των

. Το ίδιο και τα

. Ειδικότερα

άρτιος.
Χωρίζουμε τώρα το άθροισμα στα δύο: Το επιμέρους άθροισμα στα μαύρα τετραγωνάκια και αντίστοιχα, στα λευκά. Δηλαδή

άρτιος.
Παρατηρούμε ότι οι προσθετέοι

στο πρώτο άθροισμα (στα μαύρα) είναι άρτιοι ενώ στο δεύτερο, περιττοί.
Αφού όλο το άθροισμα είναι άρτιος σημαίνει ότι και το

είναι άρτιος, που με τη σειρά του σημαίνει ότι το πλήθος των πύργων που βρίσκονται σε λευκά τετράγωνα είναι άρτιος αριθμός. Έπεται ότι οι πύργοι τα μαύρα τετράγωνα είναι

μείον το πλήθος των λευκών, ίσον κάποιος περιττός.
Τώρα, με την κίνηση του ίππου, ένα πύργος πηγαίνει από λευκό τετράγωνο σε μαύρο, και αντίστροφα. Συνεπώς δεν μπορεί οι πύργοι να μην απειλούνται γιατί τότε το αντίστοιχο άθροισμα
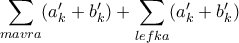
θα έπρεπε να ήταν άρτιος και άρα τα λευκά να είναι άρτιου πλήθους. Όμως τώρα είναι περιττού, όσα τα μαύρα στην αρχική διάταξη.
 σκακιέρα είναι τοποθετημένοι
σκακιέρα είναι τοποθετημένοι  πύργοι ώστε να μην απειλούνται μεταξύ τους.
πύργοι ώστε να μην απειλούνται μεταξύ τους. σκακιέρα είναι τοποθετημένοι
σκακιέρα είναι τοποθετημένοι  πύργοι ώστε να μην απειλούνται μεταξύ τους.
πύργοι ώστε να μην απειλούνται μεταξύ τους. μέχρι το πάνω δεξιά
μέχρι το πάνω δεξιά  . Αν θεωρήσουμε ότι το
. Αν θεωρήσουμε ότι το  με
με  άρτιος.
άρτιος.  . Αφού οι πύργοι δεν απειλούνται, σημαίνει ότι οι αριθμοί
. Αφού οι πύργοι δεν απειλούνται, σημαίνει ότι οι αριθμοί  είναι αναδιάταξη των
είναι αναδιάταξη των  . Το ίδιο και τα
. Το ίδιο και τα  . Ειδικότερα
. Ειδικότερα  άρτιος.
άρτιος.  άρτιος.
άρτιος. στο πρώτο άθροισμα (στα μαύρα) είναι άρτιοι ενώ στο δεύτερο, περιττοί.
στο πρώτο άθροισμα (στα μαύρα) είναι άρτιοι ενώ στο δεύτερο, περιττοί.  είναι άρτιος, που με τη σειρά του σημαίνει ότι το πλήθος των πύργων που βρίσκονται σε λευκά τετράγωνα είναι άρτιος αριθμός. Έπεται ότι οι πύργοι τα μαύρα τετράγωνα είναι
είναι άρτιος, που με τη σειρά του σημαίνει ότι το πλήθος των πύργων που βρίσκονται σε λευκά τετράγωνα είναι άρτιος αριθμός. Έπεται ότι οι πύργοι τα μαύρα τετράγωνα είναι 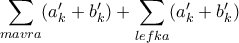
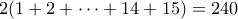 .
. ή
ή  .
. .
. περιττές στήλες και
περιττές στήλες και  άρτιες.) Αλλιώς η αρτιότητα μένει η ίδια. Θα έχουμε οπότε περιττό αριθμό αλλαγών, άτοπο.
άρτιες.) Αλλιώς η αρτιότητα μένει η ίδια. Θα έχουμε οπότε περιττό αριθμό αλλαγών, άτοπο. σκακιέρα είναι τοποθετημένοι
σκακιέρα είναι τοποθετημένοι  πύργοι ώστε να μην απειλούνται μεταξύ τους τότε αν μεταφερθεί ένας πύργος σε κελί διαφορετικό απτό δικό του θα ισχύει το ζητούμενο.
πύργοι ώστε να μην απειλούνται μεταξύ τους τότε αν μεταφερθεί ένας πύργος σε κελί διαφορετικό απτό δικό του θα ισχύει το ζητούμενο.