Al.Koutsouridis έγραψε: ↑Τετ Νοέμ 23, 2022 9:17 pm
Τα ψηφία της άπειρης ακολουθίας
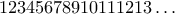
, που προκύπτει γράφοντας όλους τους φυσικούς αριθμούς, αθροίζονται εναλλάξ στις διαφορετικές πλευρές μιας τραμπάλας: το ψηφίο

στην αριστερή πλευρά, το ψηφίο

στην δεξιά, το ψηφίο

στην αριστερή κ.ο.κ. Αν σε κάθε επόμενο βήμα το άθροισμα των ψηφίων σε μια πλευρά της τραμπάλας προκύψει μεγαλύτερο, τότε αυτή γέρνει προς αυτή την πλευρά. Αληθεύει άραγε, ότι η τραμπάλα θα ταλαντεύεται εσαεί;
(Kαι για JBMO )
Η απάντηση είναι ναι,
τα ψηφία της ακολουθίας χωρίζονται σε δύο ομάδες, αυτά που είναι σε θέση με περιττό δείκτη (ομάδα

) και αυτά με άρτιο(ομάδα

).
Θα δείξω ότι για κάθε

φυσικό, όταν τα ψηφία του

είναι να εμφανιστούν στην ακολουθία τότε ο πρώτος άσσος θα ανήκει στην ομάδα

.
Για

είναι αληθές αφού η ομάδα

ξεκινά
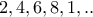
Επίσης παρατηρούμε ότι όταν οι αριθμοί

με

γραφούν στην σειρά στην δεκαδική τους αναπαράσταση τότε έχουμε σύνολο

ψηφία και τελικά όταν γράψουμε τον

ο άσσος στην αρχή θα ανήκει και πάλι στην ομάδα

και επαγωγικά έχουμε το ζητούμενο,
Για τα επόμενα βήματα της λύσης θα χρειαστούμε τις ακόλουθες παρατηρήσεις,
- Το άθροισμα των αθροισμάτων των ψηφίων όλων των θετικών ακεραίων με το πολύ
 ψηφία είναι
ψηφία είναι 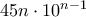
Αυτό προκύπτει ως εξής, θεωρούμε τις  θέσεις
θέσεις  , τα
, τα  και έτσι έχουμε
και έτσι έχουμε  πιθανούς συνδυασμούς.
πιθανούς συνδυασμούς.
Συνολικά στους  αυτούς αριθμούς θα έχουμε
αυτούς αριθμούς θα έχουμε  ψηφία, λόγω "συμμετρίας" το κάθε ψηφίο εμφανίζεται τον ίδιο αριθμό φορώ, έτσι τελικά κάθε ψηφίο εμφανίζεται συνολικά
ψηφία, λόγω "συμμετρίας" το κάθε ψηφίο εμφανίζεται τον ίδιο αριθμό φορώ, έτσι τελικά κάθε ψηφίο εμφανίζεται συνολικά  φορές και το ζητούμενο άθροισμα είναι
φορές και το ζητούμενο άθροισμα είναι  .
.
- Το άθροισμα των αθροισμάτων των ψηφίων όλων των θετικών ακεραίων με ακριβώς
 ψηφία είναι
ψηφία είναι 
Αυτό προκύπτει ως εξής, από το 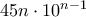 πρέπει να αγνοήσουμε όλους εκείνους τους αριθμούς που ξεκινούν με
πρέπει να αγνοήσουμε όλους εκείνους τους αριθμούς που ξεκινούν με  , οι οποίοι συνολικά θα έχουν άθροισμα αθροισμάτων ψηφίων
, οι οποίοι συνολικά θα έχουν άθροισμα αθροισμάτων ψηφίων  . Άρα ο ζητούμενος αριθμός είναι ίσος με
. Άρα ο ζητούμενος αριθμός είναι ίσος με 
Τώρα ας πάρουμε

περιττό και να δούμε στο μπλοκ

ποια ομάδα θα έχει κέρδος και πόσο είναι αυτό.
Ο

είναι περιττός έτσι καθένας από τους παραπάνω αριθμούς έχει άρτιο πλήθος ψηφίων (

) και έτσι κάθε πρώτο ψηφίο αριθμού που εμφανίζεται ανήκει στην ομάδα

. Έστω
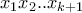
η γενική μορφή των παραπάνω αριθμών.
Το άθροισμα όλων των ψηφίων στην σειρά που θα εμφανιστούν είναι

και στην ομάδα θα καταμετρηθεί το άθροισμα

αφού ουσιαστικά μετράμε το άθροισμα των αθροισμάτων των ψηφίων των

ψήφιων αριθμών το καθένα
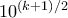
φορές, όσοι δηλαδή οι διαφορετικοί που μπορούμε να επιλέξουμε τα

με

άρτιο.
Έτσι λοιπόν από αυτό το μπλοκ η ομάδα

βγαίνει κερδισμένη κατά
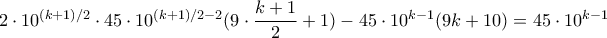
.
Τώρα ας πάρουμε το

άρτιο και κοιτάμε το ίδιο μπλόκ. Η ομάδα

αυτή τη φορά θα διατρέχει τα ψηφία

όταν

άρτιος και τα

αλλιώς (αυτό γιατί τώρα το

είναι περιττός).
Από τους αριθμούς με

άρτιο παίρνω τον

-ψήφιο

, τα

μπορούν να επιλεγούν με συνολικά
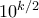
τρόπους ενώ τα
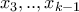
με

, το

με

και τέλος το

με

. Από εδώ έχουμε λοιπόν μια συνεισφορά

.
Από τους αριθμούς με

περιττό τα

σχηματίζουν όταν μπουν στην σειρά έναν το πολύ

- ψήφιο και τα υπόλοιπα ψηφία μπορούν να επιλεγούν με συνολικά

τρόπους άρα έχουμε στην ομάδα

μια συνεισφορά

Συνολικά λοιπόν έχουμε για την

άθροισμα ψηφίων

.
Συνεπώς αυτή τη φορά η ομάδα

βγαίνει κερδισμένη κατά

.
Άρα λοιπόν καθώς κινούμαστε προς τα δεξιά στην ακολουθία, και στα σημεία όπου συναντούμε το τελευταίο ψηφίο αριθμού της μορφής

η διαφορά

στην ζυγαριά παίρνει τιμές

και είναι απλό να δούμε γιατί ο μεγαλύτερος όρος κάθε φορά καθορίζει το πρόσημο ανεξάρτητα των προηγούμενων(οι οποίοι είναι πάντα σχετικά μικροί με αυτόν).
Εφόσον λοιπόν το πρόσημο θα εναλλάσσεται για πάντα η ζυγαριά πρέπει να ταλαντεύεται στην αιωνιότητα

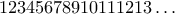 , που προκύπτει γράφοντας όλους τους φυσικούς αριθμούς, αθροίζονται εναλλάξ στις διαφορετικές πλευρές μιας τραμπάλας: το ψηφίο
, που προκύπτει γράφοντας όλους τους φυσικούς αριθμούς, αθροίζονται εναλλάξ στις διαφορετικές πλευρές μιας τραμπάλας: το ψηφίο  στην αριστερή πλευρά, το ψηφίο
στην αριστερή πλευρά, το ψηφίο  στην δεξιά, το ψηφίο
στην δεξιά, το ψηφίο  στην αριστερή κ.ο.κ. Αν σε κάθε επόμενο βήμα το άθροισμα των ψηφίων σε μια πλευρά της τραμπάλας προκύψει μεγαλύτερο, τότε αυτή γέρνει προς αυτή την πλευρά. Αληθεύει άραγε, ότι η τραμπάλα θα ταλαντεύεται εσαεί;
στην αριστερή κ.ο.κ. Αν σε κάθε επόμενο βήμα το άθροισμα των ψηφίων σε μια πλευρά της τραμπάλας προκύψει μεγαλύτερο, τότε αυτή γέρνει προς αυτή την πλευρά. Αληθεύει άραγε, ότι η τραμπάλα θα ταλαντεύεται εσαεί; 
 ) και αυτά με άρτιο(ομάδα
) και αυτά με άρτιο(ομάδα  ).
). φυσικό, όταν τα ψηφία του
φυσικό, όταν τα ψηφία του  είναι να εμφανιστούν στην ακολουθία τότε ο πρώτος άσσος θα ανήκει στην ομάδα
είναι να εμφανιστούν στην ακολουθία τότε ο πρώτος άσσος θα ανήκει στην ομάδα  είναι αληθές αφού η ομάδα
είναι αληθές αφού η ομάδα 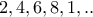 Επίσης παρατηρούμε ότι όταν οι αριθμοί
Επίσης παρατηρούμε ότι όταν οι αριθμοί  με
με  γραφούν στην σειρά στην δεκαδική τους αναπαράσταση τότε έχουμε σύνολο
γραφούν στην σειρά στην δεκαδική τους αναπαράσταση τότε έχουμε σύνολο  ψηφία και τελικά όταν γράψουμε τον
ψηφία και τελικά όταν γράψουμε τον  ο άσσος στην αρχή θα ανήκει και πάλι στην ομάδα
ο άσσος στην αρχή θα ανήκει και πάλι στην ομάδα  ψηφία είναι
ψηφία είναι 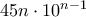
 , τα
, τα  και έτσι έχουμε
και έτσι έχουμε  πιθανούς συνδυασμούς.
πιθανούς συνδυασμούς. ψηφία, λόγω "συμμετρίας" το κάθε ψηφίο εμφανίζεται τον ίδιο αριθμό φορώ, έτσι τελικά κάθε ψηφίο εμφανίζεται συνολικά
ψηφία, λόγω "συμμετρίας" το κάθε ψηφίο εμφανίζεται τον ίδιο αριθμό φορώ, έτσι τελικά κάθε ψηφίο εμφανίζεται συνολικά  φορές και το ζητούμενο άθροισμα είναι
φορές και το ζητούμενο άθροισμα είναι  .
.
 , οι οποίοι συνολικά θα έχουν άθροισμα αθροισμάτων ψηφίων
, οι οποίοι συνολικά θα έχουν άθροισμα αθροισμάτων ψηφίων  . Άρα ο ζητούμενος αριθμός είναι ίσος με
. Άρα ο ζητούμενος αριθμός είναι ίσος με 
 ποια ομάδα θα έχει κέρδος και πόσο είναι αυτό.
ποια ομάδα θα έχει κέρδος και πόσο είναι αυτό. ) και έτσι κάθε πρώτο ψηφίο αριθμού που εμφανίζεται ανήκει στην ομάδα
) και έτσι κάθε πρώτο ψηφίο αριθμού που εμφανίζεται ανήκει στην ομάδα 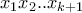 η γενική μορφή των παραπάνω αριθμών.
η γενική μορφή των παραπάνω αριθμών. και στην ομάδα θα καταμετρηθεί το άθροισμα
και στην ομάδα θα καταμετρηθεί το άθροισμα  αφού ουσιαστικά μετράμε το άθροισμα των αθροισμάτων των ψηφίων των
αφού ουσιαστικά μετράμε το άθροισμα των αθροισμάτων των ψηφίων των  ψήφιων αριθμών το καθένα
ψήφιων αριθμών το καθένα 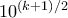 φορές, όσοι δηλαδή οι διαφορετικοί που μπορούμε να επιλέξουμε τα
φορές, όσοι δηλαδή οι διαφορετικοί που μπορούμε να επιλέξουμε τα  με
με  άρτιο.
άρτιο.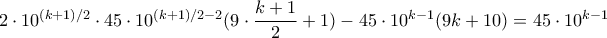 .
. όταν
όταν  άρτιος και τα
άρτιος και τα  αλλιώς (αυτό γιατί τώρα το
αλλιώς (αυτό γιατί τώρα το  -ψήφιο
-ψήφιο  , τα
, τα  μπορούν να επιλεγούν με συνολικά
μπορούν να επιλεγούν με συνολικά 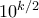 τρόπους ενώ τα
τρόπους ενώ τα 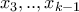 με
με  , το
, το  με
με  και τέλος το
και τέλος το  . Από εδώ έχουμε λοιπόν μια συνεισφορά
. Από εδώ έχουμε λοιπόν μια συνεισφορά  .
. - ψήφιο και τα υπόλοιπα ψηφία μπορούν να επιλεγούν με συνολικά
- ψήφιο και τα υπόλοιπα ψηφία μπορούν να επιλεγούν με συνολικά  τρόπους άρα έχουμε στην ομάδα
τρόπους άρα έχουμε στην ομάδα 
 .
. .
. η διαφορά
η διαφορά  στην ζυγαριά παίρνει τιμές
στην ζυγαριά παίρνει τιμές  και είναι απλό να δούμε γιατί ο μεγαλύτερος όρος κάθε φορά καθορίζει το πρόσημο ανεξάρτητα των προηγούμενων(οι οποίοι είναι πάντα σχετικά μικροί με αυτόν).
και είναι απλό να δούμε γιατί ο μεγαλύτερος όρος κάθε φορά καθορίζει το πρόσημο ανεξάρτητα των προηγούμενων(οι οποίοι είναι πάντα σχετικά μικροί με αυτόν).