 θετική ακέραιοι και έστω
θετική ακέραιοι και έστω  με
με  πρώτο να αποδειχθεί ότι:
πρώτο να αποδειχθεί ότι: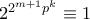 (modp^(k+1))
(modp^(k+1))Και πώς ο
 είναι μικρότερος
είναι μικρότερος  για τον οποίο ισχύει:
για τον οποίο ισχύει:  (modp^(k+1))
(modp^(k+1))Συντονιστές: cretanman, silouan, rek2

 το οποίο προκύπτει από
το οποίο προκύπτει από  αφού
αφού 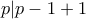 έτσι
έτσι 
 και
και  ο μικρότερος με
ο μικρότερος με  .
. άρα
άρα 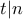 . Επιπλέον
. Επιπλέον  αλλά
αλλά  έτσι
έτσι  αλλά
αλλά  που σημαίνει
που σημαίνει  άρα
άρα 
 τότε προκύπτει
τότε προκύπτει  άρα πρέπει
άρα πρέπει  δηλαδή
δηλαδή  .
. και υποθέτοντας ότι δεν ισχύει το ζητούμενο θεωρούμε
και υποθέτοντας ότι δεν ισχύει το ζητούμενο θεωρούμε 
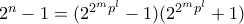 και
και 
 άτοπο!
άτοπο!Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες