 , για τον οποίο υπάρχουν θετικοί ακέραιοι
, για τον οποίο υπάρχουν θετικοί ακέραιοι  τέτοιοι, ώστε
τέτοιοι, ώστε

Συντονιστές: cretanman, silouan, rek2
 , για τον οποίο υπάρχουν θετικοί ακέραιοι
, για τον οποίο υπάρχουν θετικοί ακέραιοι  τέτοιοι, ώστε
τέτοιοι, ώστε

 .
. . Θέτουμε
. Θέτουμε  και η εξίσωση μετά τις πράξεις γίνεται:
και η εξίσωση μετά τις πράξεις γίνεται:
 απ' όπου πρέπει
απ' όπου πρέπει  με
με  .
. και επειδή οι μόνοι διαιρέτες του
και επειδή οι μόνοι διαιρέτες του  είναι οι
είναι οι  και
και  και το άθροισμα των
και το άθροισμα των  είναι άρτιος, οι μόνες περιπτώσεις για τους παράγοντες
είναι άρτιος, οι μόνες περιπτώσεις για τους παράγοντες  ώστε να ισχύει η
ώστε να ισχύει η  είναι:
είναι: ή
ή 
 βγάζουμε εύκολα τη λύση
βγάζουμε εύκολα τη λύση  .
. οπότε από την εξίσωση (1) παίρνουμε:
οπότε από την εξίσωση (1) παίρνουμε: ή
ή  .
. δηλαδή
δηλαδή  (για την οποία υπάρχουν
(για την οποία υπάρχουν  όπως έχουμε ήδη βρει παραπάνω),
όπως έχουμε ήδη βρει παραπάνω),  (απ' όπου παίρνουμε τη λύση
(απ' όπου παίρνουμε τη λύση  ) και
) και  (απ' όπου παίρνουμε
(απ' όπου παίρνουμε  ) ενώ στη 2η περίπτωση παίρνουμε
) ενώ στη 2η περίπτωση παίρνουμε  δηλαδή
δηλαδή  (για την όποια ήδη έχουμε βρει
(για την όποια ήδη έχουμε βρει  που να την ικανοποιούν).
που να την ικανοποιούν). για τον οποίο υπάρχουν
για τον οποίο υπάρχουν  που να ικανοποιούν την αρχική εξίσωση είναι ο
που να ικανοποιούν την αρχική εξίσωση είναι ο  .
.Θα μπορούσαμε να τελειώσουμε ως εξής:
 είναι Πυθαγόρεια τριάδα.
είναι Πυθαγόρεια τριάδα.Εύκολα έχουμε ότι,emouroukos έγραψε: ↑Τρί Φεβ 18, 2020 12:05 amΝα βρείτε τον μεγαλύτερο πρώτο αριθμό, για τον οποίο υπάρχουν θετικοί ακέραιοι
τέτοιοι, ώστε

 (1).
(1). . Αποδεικνύω το εξής Λήμμα :
. Αποδεικνύω το εξής Λήμμα : .
.  , οπότε υπάρχει πρώτος
, οπότε υπάρχει πρώτος  ώστε
ώστε  και
και  , οπότε αφού και ο
, οπότε αφού και ο  είναι πρώτος,
είναι πρώτος,  , άτοπο.
, άτοπο. . Οπότε,
. Οπότε,  .
. και αφού
και αφού  από το Λήμμα, έχω ότι
από το Λήμμα, έχω ότι  .
. και δοκιμάζοντας τις πιθανές περιπτώσεις έχουμε άτοπο.
και δοκιμάζοντας τις πιθανές περιπτώσεις έχουμε άτοπο. , οπότε
, οπότε  αφού
αφού  πρώτος. Έστω
πρώτος. Έστω  με
με 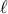 φυσικό.
φυσικό. .
. Αν
Αν 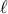 περιττός, τότε
περιττός, τότε  , οπότε,
, οπότε,  , οπότε
, οπότε  .
. , οπότε
, οπότε  .
. .
. Αν
Αν  με
με  φυσικό, τότε
φυσικό, τότε  , και αφού
, και αφού  , έχουμε
, έχουμε  , άρα
, άρα  .
. (οι πρώτες 3 απορρίπτονται άμεσα, η τέταρτη δίνει
(οι πρώτες 3 απορρίπτονται άμεσα, η τέταρτη δίνει  , άρα
, άρα  , η πέμπτη δίνει
, η πέμπτη δίνει  οπότε
οπότε  περιττός και
περιττός και  , άτοπο. Ομοίως η
, άτοπο. Ομοίως η  δίνει ως λύση την
δίνει ως λύση την  ).
). είναι
είναι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης