 που είναι τέλεια τετράγωνα, με n φυσικό.
που είναι τέλεια τετράγωνα, με n φυσικό.Πρόκειται για πρόβλημα που βρήκα στο aops, αλλά κανείς δεν έχει δημοσιεύσει λύση.
Συντονιστές: cretanman, silouan, rek2
 που είναι τέλεια τετράγωνα, με n φυσικό.
που είναι τέλεια τετράγωνα, με n φυσικό.![\mathbb{Z}[\sqrt{3}] \mathbb{Z}[\sqrt{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/afee81af192e1bcdd14caa0eeeb573f3.png) υπάρχουν άπειρες μονάδες.
υπάρχουν άπειρες μονάδες.
 περιττό.
περιττό. παραγοντοποιείται σε
παραγοντοποιείται σε  .
.![Z[\sqrt{3}] Z[\sqrt{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/756cb3176916f61c8a207f8d2305a840.png) είναι UFD).
είναι UFD). βγαίνουν πρώτα μεταξύ τους:Αν
βγαίνουν πρώτα μεταξύ τους:Αν ένας κοινός διαιρέτης τους τότε η νόρμα του θα διαιρεί το
ένας κοινός διαιρέτης τους τότε η νόρμα του θα διαιρεί το  ,ενώ παράλληλα
,ενώ παράλληλα  και άρα η νόρμα του διαιρεί το 12,δηλαδή
και άρα η νόρμα του διαιρεί το 12,δηλαδή  μονάδα.
μονάδα. ή
ή  όπου
όπου  μονάδα και
μονάδα και  η συζυγής της.
η συζυγής της. περιττό):
περιττό): .
. δηλαδή
δηλαδή  δηλαδή για
δηλαδή για  διάφορο του
διάφορο του  ,
, .Όμως τα
.Όμως τα  είναι λύσεις της (
είναι λύσεις της ( )
)  και συνεπώς ο λόγος
και συνεπώς ο λόγος  προσεγγίζει το
προσεγγίζει το  (μάλιστα για θετικά
(μάλιστα για θετικά  η μεγαλύτερη τιμή που θα πάρει είναι το
η μεγαλύτερη τιμή που θα πάρει είναι το  ).Έτσι για
).Έτσι για  σίγουρα δεν υπάρχουν λύσεις ενώ τις υπόλοιπες περιπτώσεις τις τσεκάρουμε με το χέρι από όπου παίρνουμε και την
σίγουρα δεν υπάρχουν λύσεις ενώ τις υπόλοιπες περιπτώσεις τις τσεκάρουμε με το χέρι από όπου παίρνουμε και την  .
. Έστω ότι n=2k. Τότε,
Έστω ότι n=2k. Τότε,  , ή
, ή 
 και
και 
 είναι στην ουσία 12b+1+3=12b+4, όπου το b είναι πολ4 (αυτό προκύπτει αν εφαρμόσω το ανάπτυγμα του Newton).
είναι στην ουσία 12b+1+3=12b+4, όπου το b είναι πολ4 (αυτό προκύπτει αν εφαρμόσω το ανάπτυγμα του Newton). , δηλαδή
, δηλαδή  , άρα m περιττός.
, άρα m περιττός. με το 16 είναι-3,9,5,1,-3...αντίστοιχα.
με το 16 είναι-3,9,5,1,-3...αντίστοιχα. ο εκθέτης πρέπει να είναι 5,9,13... και το
ο εκθέτης πρέπει να είναι 5,9,13... και το  θα είναι πολ16.
θα είναι πολ16. , δηλαδή το
, δηλαδή το είναι το 2 (δηλαδή ο αριθμός 4). Άρα, το 16 δεν μπορεί να διαιρεί το
είναι το 2 (δηλαδή ο αριθμός 4). Άρα, το 16 δεν μπορεί να διαιρεί το  .
.Καλωσήρθες στο
 είναι περιττός, η μέγιστη δύναμη του
είναι περιττός, η μέγιστη δύναμη του  που διαιρεί το
που διαιρεί το  είναι το
είναι το  , οπότε το
, οπότε το  πρακτικά είναι περιττός.
πρακτικά είναι περιττός. .
. αλλά του
αλλά του 

 το έγραψες
το έγραψες  , άρα το
, άρα το  αναφερόταν στο
αναφερόταν στο  , δηλαδή (υποθέτω) εννοούσες
, δηλαδή (υποθέτω) εννοούσες  . Εδώ το
. Εδώ το  προκύπτει περιττό για περιττό
προκύπτει περιττό για περιττό  (LTE)
(LTE)min## έγραψε: ↑Τρί Μάιος 28, 2019 7:11 pmΠαίρνοντας την πρώτη περίπτωση και αθροίζοντας/αφαιρώντας τις δύο σχέσεις και εξισώνοντας τους συντελεστές έχουμε (περιττό):
.
Έτσι π.χ.δηλαδή
δηλαδή για
διάφορο του
,
.Όμως τα
είναι λύσεις της (
)
και συνεπώς ο λόγος
προσεγγίζει το
(μάλιστα για θετικά
η μεγαλύτερη τιμή που θα πάρει είναι το
).Έτσι για
σίγουρα δεν υπάρχουν λύσεις ενώ τις υπόλοιπες περιπτώσεις τις τσεκάρουμε με το χέρι από όπου παίρνουμε και την
.
Η άλλη περίπτωση δε βγάζει λύση.
Που έχω λάθος;
 και όχι
και όχι  ) τα οποία όμως δεν είναι σημαντικά, νομίζω το κυριότερο πρόβλημα είναι ότι ξεχάστηκαν οι διωνυμικοί συντελεστές. Στο πρώτο άθροισμα λείπουν τα
) τα οποία όμως δεν είναι σημαντικά, νομίζω το κυριότερο πρόβλημα είναι ότι ξεχάστηκαν οι διωνυμικοί συντελεστές. Στο πρώτο άθροισμα λείπουν τα  και στο δεύτερο τα
και στο δεύτερο τα  . Αυτό χαλάει το γεγονός ότι το ένα είναι τετραπλάσιο του άλλου.
. Αυτό χαλάει το γεγονός ότι το ένα είναι τετραπλάσιο του άλλου.Demetres έγραψε: ↑Τετ Μάιος 29, 2019 9:57 ammin## έγραψε: ↑Τρί Μάιος 28, 2019 7:11 pmΠαίρνοντας την πρώτη περίπτωση και αθροίζοντας/αφαιρώντας τις δύο σχέσεις και εξισώνοντας τους συντελεστές έχουμε (περιττό):
.
Έτσι π.χ.δηλαδή
δηλαδή για
διάφορο του
,
.Όμως τα
είναι λύσεις της (
)
και συνεπώς ο λόγος
προσεγγίζει το
(μάλιστα για θετικά
η μεγαλύτερη τιμή που θα πάρει είναι το
).Έτσι για
σίγουρα δεν υπάρχουν λύσεις ενώ τις υπόλοιπες περιπτώσεις τις τσεκάρουμε με το χέρι από όπου παίρνουμε και την
.
Η άλλη περίπτωση δε βγάζει λύση.
Που έχω λάθος;
Η αλήθεια είναι ότι φοβήθηκα να το δοκιμάσω. Πέραν κάποιων λάνθασμένων προσήμων (είναι π.χ.και όχι
) τα οποία όμως δεν είναι σημαντικά, νομίζω το κυριότερο πρόβλημα είναι ότι ξεχάστηκαν οι διωνυμικοί συντελεστές. Στο πρώτο άθροισμα λείπουν τα
και στο δεύτερο τα
. Αυτό χαλάει το γεγονός ότι το ένα είναι τετραπλάσιο του άλλου.
 και ύστερα είναι εύκολο (με υπολογιστή) να βρούμε τις λύσεις. Πιστεύω να βρω χρόνο μέσα στο ΣΚ να γράψω τις λεπτομέρειες.
και ύστερα είναι εύκολο (με υπολογιστή) να βρούμε τις λύσεις. Πιστεύω να βρω χρόνο μέσα στο ΣΚ να γράψω τις λεπτομέρειες.
 τότε προκύπτει εύκολα η λύση
τότε προκύπτει εύκολα η λύση  .
. :
:



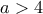 . Τότε αφού
. Τότε αφού 

 (αφού από την υπόθεση
(αφού από την υπόθεση 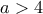 τότε
τότε  και άρα
και άρα  ). Η
). Η  γίνεται:
γίνεται:

 ως διαδοχικοί άρτιοι.
ως διαδοχικοί άρτιοι.
 .
.  .
. και
και  τότε:
τότε: ή
ή 

 .
.
 ή
ή 



 η ανίσωση μετατρέπεται στην:
η ανίσωση μετατρέπεται στην:
 που είναι άτοπο.
που είναι άτοπο. οπότε δεν ισχύει η αρχική υπόθεση
οπότε δεν ισχύει η αρχική υπόθεση 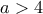 .
. απ' όπου εύκολα λαμβάνουμε τη λύση
απ' όπου εύκολα λαμβάνουμε τη λύση  .
.Δεν είναι σωστό. Ουσιαστικά λες ότι ανmiltosk έγραψε: ↑Τετ Μάιος 29, 2019 9:11 pmΚαλησπέρα. Όντας νέο μέλος παρακαλώ συγχωρέστε τα οποιαδήποτε λάθη σε Latex και αν υπάρχει λάθος παρακαλώ να αναφερθεί.
Έστω:
Αντότε προκύπτει εύκολα η λύση
.
Αν:

Ακόμη:
Έστω. Τότε αφού

Έστω(αφού από την υπόθεση
τότε
και άρα
). Η
γίνεται:
Έστω:
Τότεως διαδοχικοί άρτιοι.
Τότε:
Έστω.
Τότε.
Αφούκαι
τότε:
ή
Άτοπο καθώς
Οπότε:.
Άρα:
Ομοίως:ή
Έστω:
Τότε:
Αντικαθιστώντας όπουη ανίσωση μετατρέπεται στην:
Λύνοντας αρκεί:που είναι άτοπο.
Άρα έχουμε ότι:οπότε δεν ισχύει η αρχική υπόθεση
.
Επομένωςαπ' όπου εύκολα λαμβάνουμε τη λύση
.
 με
με 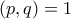 τότε
τότε  ή
ή  . Βάλε όπου
. Βάλε όπου  το
το  ,
, 
 ,
, 
 .
.Έχεις απόλυτο δίκιο. Θα προσπαθήσω να δω αν γίνεται να αποδειχθεί αυτό υπό κάποιες συνθήκες διαφορετικά μάλλον θα πρέπει να απορριφθεί η λύση.JimNt. έγραψε: ↑Τετ Μάιος 29, 2019 9:48 pmΔεν είναι σωστό. Ουσιαστικά λες ότι ανmiltosk έγραψε: ↑Τετ Μάιος 29, 2019 9:11 pmΚαλησπέρα. Όντας νέο μέλος παρακαλώ συγχωρέστε τα οποιαδήποτε λάθη σε Latex και αν υπάρχει λάθος παρακαλώ να αναφερθεί.
Έστω:
Αντότε προκύπτει εύκολα η λύση
.
Αν:

Ακόμη:
Έστω. Τότε αφού

Έστω(αφού από την υπόθεση
τότε
και άρα
). Η
γίνεται:
Έστω:
Τότεως διαδοχικοί άρτιοι.
Τότε:
Έστω.
Τότε.
Αφούκαι
τότε:
ή
Άτοπο καθώς
Οπότε:.
Άρα:
Ομοίως:ή
Έστω:
Τότε:
Αντικαθιστώντας όπουη ανίσωση μετατρέπεται στην:
Λύνοντας αρκεί:που είναι άτοπο.
Άρα έχουμε ότι:οπότε δεν ισχύει η αρχική υπόθεση
.
Επομένωςαπ' όπου εύκολα λαμβάνουμε τη λύση
.
με
τότε
ή
. Βάλε όπου
το
,

,

.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης