
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Συντονιστές: cretanman, silouan, rek2
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Οι περιπτώσεις όπου τα  είναι αρνητικά ή ένας εκ των δύο είναι αρνητικός, είναι τετριμμένες.
είναι αρνητικά ή ένας εκ των δύο είναι αρνητικός, είναι τετριμμένες.
Αν τώρα έχουμε
έχουμε  ότι
ότι  , άρα πρέπει
, άρα πρέπει  άρτιος. Τότε όμως από την αρχική εξίσωση
άρτιος. Τότε όμως από την αρχική εξίσωση  άρτιος, άτοπο.
άρτιος, άτοπο.
Αν τώρα , έχουμε
, έχουμε  , που για
, που για  είναι άτοπο, αφού το
είναι άτοπο, αφού το  βγαίνει τετραγωνικό κατάλοιπο, οπότε
βγαίνει τετραγωνικό κατάλοιπο, οπότε  ή
ή  .
.
Αν , τότε μόνη περίπτωση
, τότε μόνη περίπτωση  .
.
 είναι αρνητικά ή ένας εκ των δύο είναι αρνητικός, είναι τετριμμένες.
είναι αρνητικά ή ένας εκ των δύο είναι αρνητικός, είναι τετριμμένες. Αν τώρα
 έχουμε
έχουμε  ότι
ότι  , άρα πρέπει
, άρα πρέπει  άρτιος. Τότε όμως από την αρχική εξίσωση
άρτιος. Τότε όμως από την αρχική εξίσωση  άρτιος, άτοπο.
άρτιος, άτοπο.Αν τώρα
 , έχουμε
, έχουμε  , που για
, που για  είναι άτοπο, αφού το
είναι άτοπο, αφού το  βγαίνει τετραγωνικό κατάλοιπο, οπότε
βγαίνει τετραγωνικό κατάλοιπο, οπότε  ή
ή  .
.Αν
 , τότε μόνη περίπτωση
, τότε μόνη περίπτωση  .
.Σιλουανός Μπραζιτίκος
Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Επειδή είναι πολύ εύκολη για senior την αλλάζω λίγο:
Να βρεθούν οι ακέραιοι για τους οποίους να ισχύει
για τους οποίους να ισχύει

Να βρεθούν οι ακέραιοι
 για τους οποίους να ισχύει
για τους οποίους να ισχύει

- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Καλημέρα
Αρχικά αν
 λύση τότε και
λύση τότε και  λύση οπότε θεωρώ
λύση οπότε θεωρώ 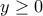
Αν
 τότε
τότε  που ισχύει μόνο για
που ισχύει μόνο για  ,
, Έστω

Αν
 τότε
τότε  άρα
άρα  , τότε όμως
, τότε όμως  άτοπο.
άτοπο.Άρα
 , αν
, αν  τότε
τότε  άτοπο, άρα
άτοπο, άρα  . Αν
. Αν  τότε
τότε  που με
που με  δίνει
δίνει  .
.Έστω τώρα

Με
 έχω
έχω  αλλά
αλλά  άρα
άρα  . Έστω
. Έστω 
Είναι
 , έστω
, έστω 
 και
και  οπότε πρέπει
οπότε πρέπει  και αφού
και αφού  θα είναι
θα είναι και
και 

Αυτή με
 δίνει
δίνει  ,θέτω
,θέτω  και έχω
και έχω  οπότε όπως και πριν πρέπει
οπότε όπως και πριν πρέπει  και
και  .
.Οπότε όλες οι λύσεις είναι

Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Μία προσπάθεια:
Προφανώς δεν υπάρχουν αρνητικοί ακέραιοι
 , που να ικανοποιούν την αρχική.
, που να ικανοποιούν την αρχική.Αν
 , τότε
, τότε  . Αν
. Αν  , τότε με
, τότε με  ,
,προκύπτει ότι
 , άτοπο. Άρα
, άτοπο. Άρα  . Για
. Για  , έχουνε την λύση
, έχουνε την λύση 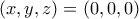 , ενώ για
, ενώ για  , έχουμε τις λύσεις
, έχουμε τις λύσεις  .
.Αν
 , τότε με
, τότε με  έχουμε ότι
έχουμε ότι  άρτιος. Έστω ότι
άρτιος. Έστω ότι  , για
, για  θετικό ακέραιο.
θετικό ακέραιο.Η εξίσωση γράφεται τώρα
 . Τότε υπάρχουν θετικοί ακέραιοι
. Τότε υπάρχουν θετικοί ακέραιοι  , με
, με  , τέτοιοι ώστε:
, τέτοιοι ώστε:

Προσθέτοντας κατά μέλη προκύπτει:
 . Διακρίνουμε τις περιπτώσεις
. Διακρίνουμε τις περιπτώσεις-
 . Τότε προφανώς παίρνουμε άτοπο.
. Τότε προφανώς παίρνουμε άτοπο. -
 . Τότε
. Τότε  , που δίνει
, που δίνει  , το οποίο μπορεί να ισχύει μόνο για
, το οποίο μπορεί να ισχύει μόνο για  . Τότε
. Τότε  ,
,  , και
, και  . Τότε
. Τότεέχουμε την λύση
 .
.-
 . Τότε θα ισχύει ότι
. Τότε θα ισχύει ότι  , το οποίο μπορεί να ισχύει μόνο για
, το οποίο μπορεί να ισχύει μόνο για  . Τότε
. Τότε  . Η εξίσωση τώρα γίνεται
. Η εξίσωση τώρα γίνεται  .
. Παίρνοντας
 λαμβάνουμε ότι
λαμβάνουμε ότι  . Που δίνει ότι
. Που δίνει ότι  περιττός. Έστω ότι
περιττός. Έστω ότι  , για
, για  θετικό ακέραιο. Η εξίσωση
θετικό ακέραιο. Η εξίσωση γράφεται:
 . Τότε υπάρχουν θετικοί ακέραιοι
. Τότε υπάρχουν θετικοί ακέραιοι  , με
, με  ,
,  , τέτοιοι ώστε:
, τέτοιοι ώστε:

Αφαιρώντας κατά μέλη παίρνουμε ότι
 . Άρα
. Άρα  , που δίνει
, που δίνει  ,
,  , και
, και , που δίνει
, που δίνει  . Τότε
. Τότε  , και συνεπώς
, και συνεπώς  . Τότε
. Τότε  , άρα
, άρα  .
.Τελικά έχουμε τις λύσεις
 .
.Παρακαλώ διορθώστε με για τυχόν λάθη, γιατί ακόμα μαθαίνω να λύνω τέτοιες ασκήσεις, και οι παρατηρήσεις σας θα με βοηθούσαν πολύ.
Edit: Με πρόλαβε ο Πρόδρομος (για αρκετή ώρα βέβαια). Το αφήνω για την πληκτρολόγηση.
Υ.Γ. Σημειώνω με έντονα γράμματα μια περίπτωση που δεν πήρα. Ευχαριστώ τον κύριο Δημήτρη για την επισήμανση!
τελευταία επεξεργασία από Joaakim σε Σάβ Ιαν 23, 2021 8:16 pm, έχει επεξεργασθεί 4 φορές συνολικά.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Αφού δείξουμε ότι τα  είναι μη αρνητικοί, βγαίνει και με modulo 8. Το αριστερό μέλος δεν είναι πολλαπλάσιο του
είναι μη αρνητικοί, βγαίνει και με modulo 8. Το αριστερό μέλος δεν είναι πολλαπλάσιο του  οπότε αναγκαστικά
οπότε αναγκαστικά  και τα πράγματα πλέον είναι εύκολα.
και τα πράγματα πλέον είναι εύκολα.
 είναι μη αρνητικοί, βγαίνει και με modulo 8. Το αριστερό μέλος δεν είναι πολλαπλάσιο του
είναι μη αρνητικοί, βγαίνει και με modulo 8. Το αριστερό μέλος δεν είναι πολλαπλάσιο του  οπότε αναγκαστικά
οπότε αναγκαστικά  και τα πράγματα πλέον είναι εύκολα.
και τα πράγματα πλέον είναι εύκολα.-
Ιωάννης Μελισσουργός
- Δημοσιεύσεις: 1
- Εγγραφή: Τετ Φεβ 14, 2024 8:47 pm
- Τοποθεσία: Αθήνα
Re: ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
Ανεβάζω και εγώ τη λύση με mod8 αν και αρκετό καιρό μετά τη δημοσίευση...
Προφανώς είναι για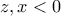 αδύνατη αφού δεν θα προκύπτει ακέραιο
αδύνατη αφού δεν θα προκύπτει ακέραιο  που να επαληθεύει τη σχέση.
που να επαληθεύει τη σχέση.
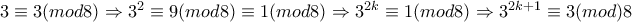
όπου
Ακόμα ισχύει ότι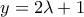 για κάποιο
για κάποιο 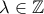 αφού το
αφού το  είναι περιττός και το
είναι περιττός και το 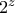
άρτιος. Επομένως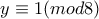 ή
ή  ή
ή  ή
ή  , απ' όπου και λαμβάνουμε ότι
, απ' όπου και λαμβάνουμε ότι  ή
ή  .
.
Παρατηρούμε λοιπόν ότι αθροίζοντας τα πιθανά υπόλοιπα των
των  και
και  προκύπτει ότι
προκύπτει ότι  που είναι άτοπο. Επομένως οι λύσεις είναι οι
που είναι άτοπο. Επομένως οι λύσεις είναι οι 
Υ.Γ. Επειδή είμαι καινούριος στο κόσμο των διαγωνιστικών μαθηματικών αν χρειάζεται κάποια διόρθωση η λύση θα χαιρόμουν πολύ να το επισημαίνατε
Προφανώς είναι για
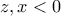 αδύνατη αφού δεν θα προκύπτει ακέραιο
αδύνατη αφού δεν θα προκύπτει ακέραιο  που να επαληθεύει τη σχέση.
που να επαληθεύει τη σχέση.
- Για
 παίρνουμε τη λύση
παίρνουμε τη λύση 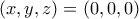
- Για
 παίρνουμε τις λύσεις
παίρνουμε τις λύσεις 
- Για
 παίρνουμε τις λύσεις
παίρνουμε τις λύσεις 
- Για
 με
με  έχουμε ότι
έχουμε ότι  ή
ή  .
.
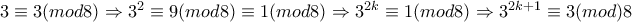
όπου

Ακόμα ισχύει ότι
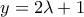 για κάποιο
για κάποιο 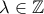 αφού το
αφού το  είναι περιττός και το
είναι περιττός και το 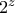
άρτιος. Επομένως
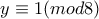 ή
ή  ή
ή  ή
ή  , απ' όπου και λαμβάνουμε ότι
, απ' όπου και λαμβάνουμε ότι  ή
ή  .
.Παρατηρούμε λοιπόν ότι αθροίζοντας τα πιθανά υπόλοιπα
 των
των  και
και  προκύπτει ότι
προκύπτει ότι  που είναι άτοπο. Επομένως οι λύσεις είναι οι
που είναι άτοπο. Επομένως οι λύσεις είναι οι 
Υ.Γ. Επειδή είμαι καινούριος στο κόσμο των διαγωνιστικών μαθηματικών αν χρειάζεται κάποια διόρθωση η λύση θα χαιρόμουν πολύ να το επισημαίνατε
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: emouroukos και 2 επισκέπτες
