 με
με  δεν διαιρούν το
δεν διαιρούν το  να λύθει ή εξίσωση
να λύθει ή εξίσωση
Συντονιστές: cretanman, silouan, rek2
 :
: , έχουμε
, έχουμε  , οπότε προκύπτει ότι
, οπότε προκύπτει ότι  , όπου
, όπου  μη αρνητικός ακέραιος.
μη αρνητικός ακέραιος. , έχουμε ότι
, έχουμε ότι  , οπότε προκύπτει ότι
, οπότε προκύπτει ότι  , όπου
, όπου  μη αρνητικός ακέραιος.
μη αρνητικός ακέραιος.  , άτοπο.
, άτοπο. περιέχεται το
περιέχεται το  , αλλά αντιμετωπίζονται εύκολα και οι υπόλοιπες περιπτώσεις:
, αλλά αντιμετωπίζονται εύκολα και οι υπόλοιπες περιπτώσεις: :
: , άτοπο από
, άτοπο από  .
. :
: , άτοπο από
, άτοπο από  .
.Διονύσιος Αδαμόπουλος έγραψε: ↑Τετ Νοέμ 07, 2018 7:52 pmΈστω:
Παίρνοντας, έχουμε
, οπότε προκύπτει ότι
, όπου
μη αρνητικός ακέραιος.
Παίρνοντας, έχουμε ότι
, οπότε προκύπτει ότι
, όπου
μη αρνητικός ακέραιος.
Άρα, άτοπο.
Δεν ξέρω αν εδώ στοπεριέχεται το
, αλλά αντιμετωπίζονται εύκολα και οι υπόλοιπες περιπτώσεις:
Έστω:
, άτοπο από
.
Έστω:
, άτοπο από
.
 διαιρεί το
διαιρεί το 
 τέτοιοι ώστε:
τέτοιοι ώστε:
 ισούται με το μηδέν έχουμε λύση.
ισούται με το μηδέν έχουμε λύση. διάφορη από το μηδέν τότε:
διάφορη από το μηδέν τότε: έχω
έχω
 έχω
έχω 
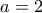 τότε:
τότε: εχω:
εχω:
 έχω:
έχω:
 τότε:
τότε: εχω:
εχω:
 .Με
.Με  έχω:
έχω:
 έχω:
έχω:
 παρατηρώ ότι:
παρατηρώ ότι:
 δεν διαιρεί το
δεν διαιρεί το 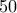
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες