Οι ρητοί είναι ακέραιοι
Δημοσιεύτηκε: Τετ Απρ 25, 2018 10:25 am
Έστω θετικοί  τέτοιοι ώστε
τέτοιοι ώστε  και ο
και ο  είναι ακέραιος για άπειρο πλήθος τιμών του
είναι ακέραιος για άπειρο πλήθος τιμών του  . Αποδείξτε ότι οι
. Αποδείξτε ότι οι 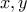 είναι ακέραιοι.
είναι ακέραιοι.
 τέτοιοι ώστε
τέτοιοι ώστε  και ο
και ο  είναι ακέραιος για άπειρο πλήθος τιμών του
είναι ακέραιος για άπειρο πλήθος τιμών του  . Αποδείξτε ότι οι
. Αποδείξτε ότι οι 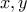 είναι ακέραιοι.
είναι ακέραιοι. .
. .
. .Τότε
.Τότε 
 .Τότε
.Τότε  , άτοπο.
, άτοπο. .
. .
. ένας πρώτος διαιρέτης του
ένας πρώτος διαιρέτης του  .
. , για άπειρα
, για άπειρα  .
. η άπειρη ακολουθία των
η άπειρη ακολουθία των 

 .
. .
. .
. .
. , άτοπο.
, άτοπο. ό.έ.δ.
ό.έ.δ.