Θα δείξουμε οτι πάλι ο Αντρέας έχει στατηγική νίκης. Θα αποδείξουμε την εξής πρόταση:
Για κάθε πίνακα

μήκους
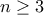
ο Αντρέας μπορεί να διαλέξει κινήσεις ώστε να δημιουργήσει σίγουρα ένα απο τα

παρακάτω ενδεχόμενα:
(i)
Ενδεχόμενο πρώτο: Τουλάχιστον ένα απο τα δύο άκρα του πίνακα είναι πολλαπλάσιο του

.
(ii)
Ενδεχόμενο δεύτερο: Όλα τα στοιχεία εκτός των δύο άκρων του πίνακα είναι πολλαπλάσια του

.
Βλέπουμε εύκολα οτι τότε συνεπάγεται οτι για κάθε πίνακα μήκους
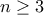
, είναι πάντα εφικτό για τον Αντρέα να κάνει όλα πλην

απο τα κελιά του πολλαπλάσια του

. Ο λόγος είναι ο εξής. Εάν ο Αντρέας δημιουργήσει το δεύτερο ενδεχόμενο τότε όλα τα στοιχεία εκτός ίσως τα δύο άκρα του πίνακα είναι πολλαπλάσια του

. Αντιθέτως, εάν πραγματοποιήσει το πρώτο ενδεχόμενο τότε μπορεί να προχωρήσει επαγωγικά στον πίνακα που αποτελείται απο όλα τα κελιά του αρχικού πλην του άκρου που έχει γίνει πολλαπλάσιο του

.
Για να αποτρέψει ο Βασίλης το πρώτο ενδεχόμενο, πρέπει να αποτρέψει την περίπτωση οπου το ένα άκρο του πίνακα ισούται με

και το δεύτερο με

. Διαφορετικά ο Αντρέας μπορεί να διαλέξει τα κελιά
![[1:n] [1:n]](/forum/ext/geomar/texintegr/latexrender/pictures/f7533719317a91c281d2606d33f3f806.png)
(θα χρησιμοποιήσω αυτόν τον συμβολισμό για να συμβολίσω οτι ο Αντρέας επέλεξε τα κελιά ανάμεσα και συμπεριλαμβανομένων του πρώτου και του n-οστού.) Τότε είτε ο Βασίλης προσθέσει είτε αφαιρέσει

θα θέσει ένα κελί στο άκρο ως πολλαπλάσιο του

και συνεπώς θα δημιουργήσει το πρώτο ενδεχόμενο που θέλει να αποτρέψει.
Θα δείξουμε οτι εάν ο Βασίλης προσπαθήσει να αποτρέψει το πρώτο ενδεχόμενο τότε ο Αντρέας μπορεί να τον υποχρεώσει να δημιουργήσει το δεύτερο ενδεχόμενο. Έστω

οι τιμές στα δύο άκρα. Τότε

και

διαφορετικά θα είμαστε στο πρώτο ενδεχόμενο.
Λήμμα: Μπορούμε να κάνουμε κινήσεις ώστε ακριβώς ένα απο τα δύο άκρα να ισούται με

χωρίς να αλλάξουμε τα ενδιάμεσα κελιά.
Απόδειξη: Εάν

τότε ο Αντρέας διαλέγει το κελί

και ο Βασίλης πρέπει να προσθέσει

στο

διαφορετικά είμαστε στο πρώτο ενδεχόμενο. Όμοια ελέγχονται και οι άλλες περιπτώσεις.
Ας υποθέσουμε λοιπόν δίχως βλάβη της γενικότητας οτι

(οι υπολοιπες περιπτώσεις λειτουργούν αντίστοιχα με αυτήν).
Ας γράψουμε τον πίνακα
![A=[a=1,l_2,...,l_{n-1},b=2] A=[a=1,l_2,...,l_{n-1},b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/b07a88d40c34887b9a4243c8b507387c.png)
όπου

. Τότε η εξής ακολουθία επαναλαμβάνεται

φορές:
(i) Ο Αντρέας επιλέγει τα κελιά
![[2:n] [2:n]](/forum/ext/geomar/texintegr/latexrender/pictures/e6079da4a49a9a56672fe6b94d278e49.png)
(ii) Ο Βασιλης αφαιρεί

απο όλα (διαφορετικά

)
(iii) Ο Αντρέας επιλέγει το άκρο

(που τώρα ισούται με

)
(iv) Ο Βασιλης προσθέτει

(διαφορετικά

).
Συνεπώς μετά απο

επαναλήψεις ο πίνακας έχει την μορφή
![A=[a=1,0,l'_{3}...,l'_{n-1},b=2] A=[a=1,0,l'_{3}...,l'_{n-1},b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/6762149a3c50469537c4184c92931a50.png)
Στην συνέχεια ο Αντρέας επαναλαμβάνει με τα κελιά
![[3:n] [3:n]](/forum/ext/geomar/texintegr/latexrender/pictures/112faedf8a8c9d8b2088b6b6c68d778e.png)
, μετά με
![[4:n] [4:n]](/forum/ext/geomar/texintegr/latexrender/pictures/1f8ac69cc8d29ecccf3f487d67f1d3b3.png)
κ.ο.κ μέχρι
![[n-1,n] [n-1,n]](/forum/ext/geomar/texintegr/latexrender/pictures/cd55025b9799e5ce196cd281cec6f100.png)
. Έτσι στο τέλος
![A=[a=1,0,0,...,0,0,b=2] A=[a=1,0,0,...,0,0,b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/ce98c0b7d53f28f1c03d9ef83ff2ce8f.png)
και συνεπώς δημιουργήσαμε το δεύτερο ενδεχόμενο.
 ακέραιοι αριθμοί. Σε κάθε βήμα ο Ανδρέας διαλέγει κάποιους συνεχόμενους αριθμούς (από
ακέραιοι αριθμοί. Σε κάθε βήμα ο Ανδρέας διαλέγει κάποιους συνεχόμενους αριθμούς (από  μέχρι
μέχρι  ) και ο Βασίλης επιλέγει είτε να προσθέσει σε όλους
) και ο Βασίλης επιλέγει είτε να προσθέσει σε όλους  είτε να αφαιρέσει από όλους
είτε να αφαιρέσει από όλους  .
.  από αυτούς τους αριθμούς (ταυτοχρόνως) πολλαπλάσια του
από αυτούς τους αριθμούς (ταυτοχρόνως) πολλαπλάσια του  ενώ σκοπός του Βασίλη είναι να τον αποτρέψει.
ενώ σκοπός του Βασίλη είναι να τον αποτρέψει.
 μήκους
μήκους 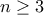 ο Αντρέας μπορεί να διαλέξει κινήσεις ώστε να δημιουργήσει σίγουρα ένα απο τα
ο Αντρέας μπορεί να διαλέξει κινήσεις ώστε να δημιουργήσει σίγουρα ένα απο τα  παρακάτω ενδεχόμενα:
παρακάτω ενδεχόμενα: και το δεύτερο με
και το δεύτερο με  . Διαφορετικά ο Αντρέας μπορεί να διαλέξει τα κελιά
. Διαφορετικά ο Αντρέας μπορεί να διαλέξει τα κελιά ![[1:n] [1:n]](/forum/ext/geomar/texintegr/latexrender/pictures/f7533719317a91c281d2606d33f3f806.png) (θα χρησιμοποιήσω αυτόν τον συμβολισμό για να συμβολίσω οτι ο Αντρέας επέλεξε τα κελιά ανάμεσα και συμπεριλαμβανομένων του πρώτου και του n-οστού.) Τότε είτε ο Βασίλης προσθέσει είτε αφαιρέσει
(θα χρησιμοποιήσω αυτόν τον συμβολισμό για να συμβολίσω οτι ο Αντρέας επέλεξε τα κελιά ανάμεσα και συμπεριλαμβανομένων του πρώτου και του n-οστού.) Τότε είτε ο Βασίλης προσθέσει είτε αφαιρέσει  οι τιμές στα δύο άκρα. Τότε
οι τιμές στα δύο άκρα. Τότε  και
και  διαφορετικά θα είμαστε στο πρώτο ενδεχόμενο.
διαφορετικά θα είμαστε στο πρώτο ενδεχόμενο. χωρίς να αλλάξουμε τα ενδιάμεσα κελιά.
χωρίς να αλλάξουμε τα ενδιάμεσα κελιά. τότε ο Αντρέας διαλέγει το κελί
τότε ο Αντρέας διαλέγει το κελί  και ο Βασίλης πρέπει να προσθέσει
και ο Βασίλης πρέπει να προσθέσει  (οι υπολοιπες περιπτώσεις λειτουργούν αντίστοιχα με αυτήν).
(οι υπολοιπες περιπτώσεις λειτουργούν αντίστοιχα με αυτήν).![A=[a=1,l_2,...,l_{n-1},b=2] A=[a=1,l_2,...,l_{n-1},b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/b07a88d40c34887b9a4243c8b507387c.png) όπου
όπου  . Τότε η εξής ακολουθία επαναλαμβάνεται
. Τότε η εξής ακολουθία επαναλαμβάνεται  φορές:
φορές:![[2:n] [2:n]](/forum/ext/geomar/texintegr/latexrender/pictures/e6079da4a49a9a56672fe6b94d278e49.png)
 )
) (που τώρα ισούται με
(που τώρα ισούται με  ).
). ![A=[a=1,0,l'_{3}...,l'_{n-1},b=2] A=[a=1,0,l'_{3}...,l'_{n-1},b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/6762149a3c50469537c4184c92931a50.png)
![[3:n] [3:n]](/forum/ext/geomar/texintegr/latexrender/pictures/112faedf8a8c9d8b2088b6b6c68d778e.png) , μετά με
, μετά με ![[4:n] [4:n]](/forum/ext/geomar/texintegr/latexrender/pictures/1f8ac69cc8d29ecccf3f487d67f1d3b3.png) κ.ο.κ μέχρι
κ.ο.κ μέχρι ![[n-1,n] [n-1,n]](/forum/ext/geomar/texintegr/latexrender/pictures/cd55025b9799e5ce196cd281cec6f100.png) . Έτσι στο τέλος
. Έτσι στο τέλος ![A=[a=1,0,0,...,0,0,b=2] A=[a=1,0,0,...,0,0,b=2]](/forum/ext/geomar/texintegr/latexrender/pictures/ce98c0b7d53f28f1c03d9ef83ff2ce8f.png) και συνεπώς δημιουργήσαμε το δεύτερο ενδεχόμενο.
και συνεπώς δημιουργήσαμε το δεύτερο ενδεχόμενο. οι αριθμοί που είναι γραμμένοι στον πίνακα (με αυτήν την σειρά). Τότε είτε μπορώ να κάνω ένα από τους
οι αριθμοί που είναι γραμμένοι στον πίνακα (με αυτήν την σειρά). Τότε είτε μπορώ να κάνω ένα από τους  πολλαπλάσιο του
πολλαπλάσιο του  .
.  τότε μπορώ να κάνω έναν από αυτούς πολλαπλάσιο του
τότε μπορώ να κάνω έναν από αυτούς πολλαπλάσιο του  αντιστοιχεί στον
αντιστοιχεί στον  , ο
, ο  στους
στους  και ο
και ο  στον
στον  .]
.] περιττούς και τον
περιττούς και τον  αφού αλλιώς τελείωσα. Αν
αφού αλλιώς τελείωσα. Αν  τότε ο ένας είναι ισότιμος με
τότε ο ένας είναι ισότιμος με  και ο άλλος με
και ο άλλος με  . Αν τώρα ο Αντρέας επιλέξει τους
. Αν τώρα ο Αντρέας επιλέξει τους  για να μην γίνει ο
για να μην γίνει ο  και
και  οπότε αν ο Αντρέας επιλέξει τους
οπότε αν ο Αντρέας επιλέξει τους 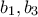 θα γίνει πολλαπλάσιο του
θα γίνει πολλαπλάσιο του  για κάποιο
για κάποιο  . Τότε είτε μπορώ να κάνω ένα από τους
. Τότε είτε μπορώ να κάνω ένα από τους  .
. . Τώρα επιλέγω αν χρειαστεί τον
. Τώρα επιλέγω αν χρειαστεί τον  ώστε να έχει διαφορετική αρτιότητα από τους
ώστε να έχει διαφορετική αρτιότητα από τους  . Άρα
. Άρα  οι αριθμοί θα είναι μιας από τις δύο πιο κάτω μορφές
οι αριθμοί θα είναι μιας από τις δύο πιο κάτω μορφές 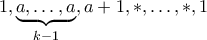

 και είτε ο
και είτε ο  .
.