 τέτοιους ώστε ο αριθμός
τέτοιους ώστε ο αριθμός  να διαιρείται από τον
να διαιρείται από τον 
Συντονιστές: cretanman, silouan, rek2
 τέτοιους ώστε ο αριθμός
τέτοιους ώστε ο αριθμός  να διαιρείται από τον
να διαιρείται από τον 
 έχω λύσεις. Θα αποδείξω ότι αν υπάρχουν λύσεις για
έχω λύσεις. Θα αποδείξω ότι αν υπάρχουν λύσεις για  τοτε ο
τοτε ο  είναι πρώτος.
είναι πρώτος. σύνθετο και
σύνθετο και  .
.  . Είναι
. Είναι  (αφού
(αφού  ) άρα
) άρα  . Είναι
. Είναι 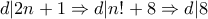 ,οπότε ο
,οπότε ο  είναι άρτιος, άτοπο αφού
είναι άρτιος, άτοπο αφού  περιττός. Άρα
περιττός. Άρα  πρώτος.
πρώτος. .
.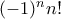 έχω
έχω 
 άρα είναι
άρα είναι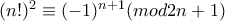
 .
. 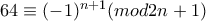


 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες