 το περίκεντρο και
το περίκεντρο και  η διάμεσος τριγώνου
η διάμεσος τριγώνου  Ο κύκλος με διάμετρο την
Ο κύκλος με διάμετρο την  και ο κύκλος που
και ο κύκλος πουδιέρχεται από τα σημεία
 τέμνονται και σε ένα δεύτερο σημείο
τέμνονται και σε ένα δεύτερο σημείο 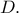 Αν οι
Αν οι  τέμνονται στο
τέμνονται στο 
να δείξετε ότι

Συντονιστές: vittasko, silouan, rek2
 το περίκεντρο και
το περίκεντρο και  η διάμεσος τριγώνου
η διάμεσος τριγώνου  Ο κύκλος με διάμετρο την
Ο κύκλος με διάμετρο την  και ο κύκλος που
και ο κύκλος που τέμνονται και σε ένα δεύτερο σημείο
τέμνονται και σε ένα δεύτερο σημείο 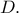 Αν οι
Αν οι  τέμνονται στο
τέμνονται στο 

Έστωgeorge visvikis έγραψε: ↑Τρί Νοέμ 29, 2022 2:06 pmΤμηματική ισότητα...png
Έστωτο περίκεντρο και
η διάμεσος τριγώνου
Ο κύκλος με διάμετρο την
και ο κύκλος που
διέρχεται από τα σημείατέμνονται και σε ένα δεύτερο σημείο
Αν οι
τέμνονται στο

να δείξετε ότι
 το σημείο τομής του κύκλου διαμέτρου
το σημείο τομής του κύκλου διαμέτρου  με την
με την  . Προφανώς
. Προφανώς  (λόγω της διαμέτρου) και
(λόγω της διαμέτρου) και  το μέσο της
το μέσο της  (
(  απόστημα στη χορδή
απόστημα στη χορδή  του
του  ) και
) και  (απόστημα στη χορδή
(απόστημα στη χορδή  , αφού
, αφού  το μέσο της) και ας είναι
το μέσο της) και ας είναι  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις  αντίστοιχα.
αντίστοιχα.  η
η 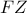 είναι ο προβολή της διαμέσου του
είναι ο προβολή της διαμέσου του  στην πλευρά του
στην πλευρά του  και συνεπώς σύμφωνα με το 2ο Θεώρημα των διαμέσων θα ισχύει:
και συνεπώς σύμφωνα με το 2ο Θεώρημα των διαμέσων θα ισχύει:  και ομοίως από το ίδιο θεώρημα στο τρίγωνο
και ομοίως από το ίδιο θεώρημα στο τρίγωνο  θα έχουμε
θα έχουμε  . Με
. Με  προκύπτει ότι τα πρώτα μέλη των ως άνω ισοτήτων είναι ίσα άρα
προκύπτει ότι τα πρώτα μέλη των ως άνω ισοτήτων είναι ίσα άρα 
 σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι
σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι  και επειδή διέρχεται από το κέντρο του περίκυκλου
και επειδή διέρχεται από το κέντρο του περίκυκλου  του
του  θα είναι μεσοκάθετος της
θα είναι μεσοκάθετος της 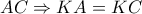 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.  Στα παραπάνω υποθέσαμε ότι το τρίγωνο είναι σκαληνό. Αν είναι ισοσκελές η πρόταση είναι προφανής
Στα παραπάνω υποθέσαμε ότι το τρίγωνο είναι σκαληνό. Αν είναι ισοσκελές η πρόταση είναι προφανήςΑς είναιgeorge visvikis έγραψε: ↑Τρί Νοέμ 29, 2022 2:06 pmΤμηματική ισότητα...png
Έστωτο περίκεντρο και
η διάμεσος τριγώνου
Ο κύκλος με διάμετρο την
και ο κύκλος που
διέρχεται από τα σημείατέμνονται και σε ένα δεύτερο σημείο
Αν οι
τέμνονται στο

να δείξετε ότι
 το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον κύκλο
στον κύκλο  .Έστω τώρα
.Έστω τώρα  το άλλο σημείο τομής του κύκλου
το άλλο σημείο τομής του κύκλου  με την
με την .
. τα
τα  είναι εφαπτόμενα τμήματα στον
είναι εφαπτόμενα τμήματα στον  και το τετράπλευρο
και το τετράπλευρο  είναι αρμονικό .
είναι αρμονικό . είναι και μέσο της χορδής
είναι και μέσο της χορδής  . Οι
. Οι  είναι οι συμετροδιάμεσοι από τα
είναι οι συμετροδιάμεσοι από τα  στα
στα  .
Έτσι έχω:
.
Έτσι έχω:  και αφού
και αφού  (βαίνουν στο ίδιο τόξο ) θα είναι :
(βαίνουν στο ίδιο τόξο ) θα είναι :




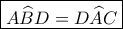 και ομοίως
και ομοίως 
 άρα η
άρα η  είναι διχοτόμος του
είναι διχοτόμος του 
 είναι
είναι  άρα η
άρα η  είναι
είναι 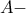 συμμετροδιάμεσος του τριγώνου
συμμετροδιάμεσος του τριγώνου  και
και 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης