 και ένα μεταβλητό σημείο
και ένα μεταβλητό σημείο  της πλευράς
της πλευράς  Επί των
Επί των  θεωρώ τα σημεία
θεωρώ τα σημεία 
αντίστοιχα, ώστε
 και
και  Να δείξετε ότι ο περίκυκλος του
Να δείξετε ότι ο περίκυκλος του  διέρχεται από σταθερό σημείο.
διέρχεται από σταθερό σημείο.Συντονιστές: vittasko, silouan, rek2
 και ένα μεταβλητό σημείο
και ένα μεταβλητό σημείο  της πλευράς
της πλευράς  Επί των
Επί των  θεωρώ τα σημεία
θεωρώ τα σημεία 
 και
και  Να δείξετε ότι ο περίκυκλος του
Να δείξετε ότι ο περίκυκλος του  διέρχεται από σταθερό σημείο.
διέρχεται από σταθερό σημείο.

 οπότε από άμεση εφαρμογή του γενικού θεωρήματος MacLaurin παίρνουμε το ζητούμενο.
οπότε από άμεση εφαρμογή του γενικού θεωρήματος MacLaurin παίρνουμε το ζητούμενο.Έστωgeorge visvikis έγραψε: ↑Παρ Νοέμ 25, 2022 12:47 pmΜε αφορμή αυτήν. Από σταθερό σημείο και αυτός..png
Δίνεται τρίγωνοκαι ένα μεταβλητό σημείο
της πλευράς
Επί των
θεωρώ τα σημεία
αντίστοιχα, ώστεκαι
Να δείξετε ότι ο περίκυκλος του
διέρχεται από σταθερό σημείο.
 το ύψος του
το ύψος του  . Προφανώς αυτό είναι σταθερό. Σταθερός είναι και ο κύκλος
. Προφανώς αυτό είναι σταθερό. Σταθερός είναι και ο κύκλος  , διαμέτρου
, διαμέτρου  .
Η από το
.
Η από το  , σταθερή παράλληλη προς την
, σταθερή παράλληλη προς την  τέμνει τον κύκλο
τέμνει τον κύκλο  στο σταθερό σημείο
στο σταθερό σημείο  και άρα η ευθεία
και άρα η ευθεία  είναι σταθερή .
είναι σταθερή . είναι μια οριακή θέση του κύκλου
είναι μια οριακή θέση του κύκλου  που διέρχεται από τα
που διέρχεται από τα  και άρα το κέντρο του θα ανήκει πάντα στην σταθερή ευθεία
και άρα το κέντρο του θα ανήκει πάντα στην σταθερή ευθεία 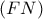 .
. το άλλο (εκτός του
το άλλο (εκτός του  ) κοινό τους σημείο , αυτό θα είναι το σταθερό συμμετρικό του
) κοινό τους σημείο , αυτό θα είναι το σταθερό συμμετρικό του  ως προς την
ως προς την  .
.edit: Διόρθωση στην αρχή απόS.E.Louridas έγραψε: ↑Παρ Νοέμ 25, 2022 1:49 pmΕν τάχει μία διαπραγμάτευση.
Έχουμε
Τελικάοπότε από άμεση εφαρμογή του γενικού θεωρήματος MacLaurin παίρνουμε το ζητούμενο.
 σε
σε 
 τέμνει τον κύκλο στο
τέμνει τον κύκλο στο 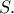 θα δείξω ότι το
θα δείξω ότι το  είναι σταθερό. Η κάθετη από το
είναι σταθερό. Η κάθετη από το  στην
στην 
 στο
στο  και η
και η  τον
τον  στο
στο 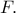 Αλλά,
Αλλά,  Άρα τα
Άρα τα  είναι
είναι
 Επομένως τα σημεία
Επομένως τα σημεία  είναι ομοκυκλικά και το
είναι ομοκυκλικά και το  ανήκει στον κύκλο που διέρχεται
ανήκει στον κύκλο που διέρχεται  και εφάπτεται της
και εφάπτεται της  στο
στο  Οπότε το
Οπότε το  ως σημείο τομής δύο σταθερών κύκλων είναι σταθερό.
ως σημείο τομής δύο σταθερών κύκλων είναι σταθερό.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης