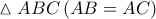 και σημείο
και σημείο  της
της  ώστε
ώστε  , όπου
, όπου  το μέσο της
το μέσο της  . Αν
. Αν 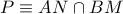 όπου
όπου  το συμμετρικό ως προς την
το συμμετρικό ως προς την  του μέσου
του μέσου  της
της  , να δείξετε ότι
, να δείξετε ότι 
Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμα
Συντονιστές: vittasko, silouan, rek2
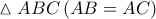 και σημείο
και σημείο  της
της  ώστε
ώστε  , όπου
, όπου  το μέσο της
το μέσο της  . Αν
. Αν 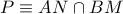 όπου
όπου  το συμμετρικό ως προς την
το συμμετρικό ως προς την  του μέσου
του μέσου  της
της  , να δείξετε ότι
, να δείξετε ότι 
Δε φέρνω ( προσωρινά) τηνΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Οκτ 29, 2022 10:43 pmΕνδιαφέρουσα εξηντάρα.png
Δίνεται ισοσκελές τρίγωνοκαι σημείο
της
ώστε
, όπου
το μέσο της
. Αν
όπου
το συμμετρικό ως προς την
του μέσου
της
, να δείξετε ότι

Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμα

 το σημείο τομής της
το σημείο τομής της  με την
με την 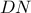 . Προφανώς
. Προφανώς  .
. παράλληλη στην
παράλληλη στην  και τέμνει την ευθεία
και τέμνει την ευθεία  στο
στο  .
Το τρίγωνο
.
Το τρίγωνο  , έτσι αν η
, έτσι αν η  τέμνει τη
τέμνει τη  στο
στο  θα είναι :
θα είναι :  ( κεντρικής δέσμης το ανάγνωσμα γάρ )
( κεντρικής δέσμης το ανάγνωσμα γάρ ) είναι ισόπλευρο και άρα τα σημεία
είναι ισόπλευρο και άρα τα σημεία  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.  συγκλίνουν σε σημείο
συγκλίνουν σε σημείο  για το οποίο, το
για το οποίο, το  είναι ισόπλευρο και
είναι ισόπλευρο και  .
Γράφω τώρα τον περιγεγραμμένο κύκλο (κόκκινο) του ισοπλεύρου
.
Γράφω τώρα τον περιγεγραμμένο κύκλο (κόκκινο) του ισοπλεύρου  και ας είναι
και ας είναι  το άλλο σημείο τομής του , με την
το άλλο σημείο τομής του , με την  .
.  .
. , το τετράπλευρο
, το τετράπλευρο  είναι εγγράψιμο ( γράφω κι αυτόν τον κύκλο (μπλέ))
είναι εγγράψιμο ( γράφω κι αυτόν τον κύκλο (μπλέ))  είναι ισόπλευρο ,
είναι ισόπλευρο ,  οπότε λόγω της
οπότε λόγω της  ,
,  .
. ανήκουν στην ίδια ευθεία και το
ανήκουν στην ίδια ευθεία και το  .
.Αν εν τέλει φέρουμε και τηνDoloros έγραψε: ↑Κυρ Οκτ 30, 2022 12:49 amΔε φέρνω ( προσωρινά) τηνΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Οκτ 29, 2022 10:43 pmΕνδιαφέρουσα εξηντάρα.png
Δίνεται ισοσκελές τρίγωνοκαι σημείο
της
ώστε
, όπου
το μέσο της
. Αν
όπου
το συμμετρικό ως προς την
του μέσου
της
, να δείξετε ότι

Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμα
Ας είναιτο σημείο τομής της
με την
. Προφανώς
.
Φέρνω από τοπαράλληλη στην
και τέμνει την ευθεία
στο
.
Ενδιαφέρουσα εξηντάρα_new_a.png
Το τρίγωνο, έτσι αν η
τέμνει τη
στο
θα είναι :
( κεντρικής δέσμης το ανάγνωσμα γάρ )
Τώρα τοείναι ισόπλευρο και άρα τα σημεία
ανήκουν στην ίδια ευθεία.
( τα υπόλοιπα που φαίνονται στο σχήμα είναι μεν προφανή αλλά ελάχιστα θα τα επικαλεστώ)
Επί της ουσίας έχει δειχθεί ότι οι ευθείεςσυγκλίνουν σε σημείο
για το οποίο, το
είναι ισόπλευρο και
.
Ενδιαφέρουσα εξηντάρα_new_b.png
 και
και  , τότε έχουμε προφανώς τα τρίγωνα
, τότε έχουμε προφανώς τα τρίγωνα  και
και 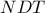 είναι ίσα, άρα
είναι ίσα, άρα  εγγράψιμο καθώς
εγγράψιμο καθώς  και άρα
και άρα 
Συνεχίζω από εκεί που ο φίλτατος Νίκος απέδειξε ότι τοΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Οκτ 29, 2022 10:43 pmΕνδιαφέρουσα εξηντάρα.png
Δίνεται ισοσκελές τρίγωνοκαι σημείο
της
ώστε
, όπου
το μέσο της
. Αν
όπου
το συμμετρικό ως προς την
του μέσου
της
, να δείξετε ότι

Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμα
 είναι ισόπλευρο.
Εξωτερικά του τριγώνου
είναι ισόπλευρο.
Εξωτερικά του τριγώνου  έχουν κατασκευαστεί τα ισόπλευρα τρίγωνα
έχουν κατασκευαστεί τα ισόπλευρα τρίγωνα 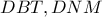 άρα οι
άρα οι  τέμνονται στο σημείο
τέμνονται στο σημείο  υπό γωνία
υπό γωνία 
george visvikis έγραψε: ↑Κυρ Οκτ 30, 2022 10:32 amΣυνεχίζω από εκεί που ο φίλτατος Νίκος απέδειξε ότι τοΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Οκτ 29, 2022 10:43 pmΕνδιαφέρουσα εξηντάρα.png
Δίνεται ισοσκελές τρίγωνοκαι σημείο
της
ώστε
, όπου
το μέσο της
. Αν
όπου
το συμμετρικό ως προς την
του μέσου
της
, να δείξετε ότι

Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμαείναι ισόπλευρο. 60αρα!!!.png
Εξωτερικά του τριγώνουέχουν κατασκευαστεί τα ισόπλευρα τρίγωνα
άρα οι
τέμνονται στο σημείο
υπό γωνία

 ,
,  τέμνουν τη
τέμνουν τη  στα σημεία
στα σημεία  ,
,  αντίστοιχα.
αντίστοιχα. το σημείο τομής των
το σημείο τομής των  και
και  ,
,  το σημείο τομής της
το σημείο τομής της 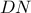 με την
με την  ,
, το σημείο τομής της
το σημείο τομής της  με την
με την  ,
,  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  , και
, και 
 και
και  .
.  .
. ,
, 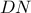 είναι συμμετρικές ως προς το ύψος
είναι συμμετρικές ως προς το ύψος  , οπότε η
, οπότε η  διχοτόμος της γωνίας
διχοτόμος της γωνίας  και
και  .
.  είναι αρμονική
είναι αρμονική  η τετράδα
η τετράδα  είναι αρμονική
είναι αρμονική  .
. προκύπτει ότι η τετράδα
προκύπτει ότι η τετράδα  είναι αρμονική
είναι αρμονική  η δέσμη
η δέσμη  είναι αρμονική, οπότε οι ακτίνες αυτής της δέσμης ορίζουν στην ευθεία
είναι αρμονική, οπότε οι ακτίνες αυτής της δέσμης ορίζουν στην ευθεία  την αρμονική τετράδα
την αρμονική τετράδα  .
. 
 και
και  έχουμε ότι
έχουμε ότι  .
. (η
(η  άξονας συμμετρίας της
άξονας συμμετρίας της 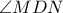 , και
, και 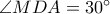 ). Το τρίγωνο
). Το τρίγωνο 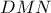 είναι προφανώς
είναι προφανώς  το τρίγωνο
το τρίγωνο  ορθογώνιο στο
ορθογώνιο στο  .
. ,
,  ,
,  .
.  είναι αρμονική, οπότε οι ακτίνες της αρμονικής δέσμης
είναι αρμονική, οπότε οι ακτίνες της αρμονικής δέσμης  ορίζουν στην ευθεία
ορίζουν στην ευθεία  την αρμονική τετράδα
την αρμονική τετράδα  .
. 
 διαγώνιος
διαγώνιος 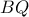 διαιρείται αρμονικά από τις δύο άλλες διαγώνιες, δηλαδή,
διαιρείται αρμονικά από τις δύο άλλες διαγώνιες, δηλαδή, είναι αρμονική.
είναι αρμονική. 
 και
και  έχουμε ότι
έχουμε ότι  .
. είναι αρμονική
είναι αρμονική  δέσμη
δέσμη  είναι αρμονική, και
είναι αρμονική, και , τότε η
, τότε η 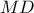 διχοτόμος της γωνίας
διχοτόμος της γωνίας  , δηλαδή,
, δηλαδή,  .
. και
και  (
(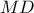 κοινή,
κοινή,  και
και  )
) , δηλαδή το τετράπλευρο
, δηλαδή το τετράπλευρο  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  .
.Από τη συμμετρία τουΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Σάβ Οκτ 29, 2022 10:43 pmΕνδιαφέρουσα εξηντάρα.png
Δίνεται ισοσκελές τρίγωνοκαι σημείο
της
ώστε
, όπου
το μέσο της
. Αν
όπου
το συμμετρικό ως προς την
του μέσου
της
, να δείξετε ότι

Υ.Σ. Παρακαλώ ολοκληρωμένες λύσεις και με σχήμα
 ως προς την
ως προς την  που είναι άξονας συμμετρίας του ισοσκελούς τριγώνου
που είναι άξονας συμμετρίας του ισοσκελούς τριγώνου  προκύπτει ότι
προκύπτει ότι  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς την
ως προς την  και συνεπώς (λόγω συμμετρίας) θα είναι
και συνεπώς (λόγω συμμετρίας) θα είναι  και
και  και με
και με  από συμμετρία προκύπτει ότι το τρίγωνο
από συμμετρία προκύπτει ότι το τρίγωνο  είναι ισόπλευρο και με
είναι ισόπλευρο και με  τα μέσα των πλευρών του
τα μέσα των πλευρών του  ομοκυκλικά με
ομοκυκλικά με 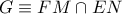 (προφανώς το κέντρο του ισοπλεύρου τριγώνου
(προφανώς το κέντρο του ισοπλεύρου τριγώνου  )
) τότε από το Θεώρημα του Μενελάου στο τρίγωνο
τότε από το Θεώρημα του Μενελάου στο τρίγωνο  με διατέμνουσα την
με διατέμνουσα την  Από τη σχέση
Από τη σχέση  προκύπτει ότι η σημειοσειρά
προκύπτει ότι η σημειοσειρά  είναι αρμονική , άρα και η δέσμη
είναι αρμονική , άρα και η δέσμη 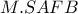 είναι αρμονική και με
είναι αρμονική και με  διχοτόμος της γωνίας
διχοτόμος της γωνίας  όμως
όμως  (συμμετρικές ως προς την
(συμμετρικές ως προς την 
 ομοκυκλικά .
ομοκυκλικά . και
και  με τρία κοινά σημεία
με τρία κοινά σημεία  προκύπτει ότι τα
προκύπτει ότι τα  είναι ομοκυκλικά και συνεπώς
είναι ομοκυκλικά και συνεπώς  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. με
με  , το
, το  είναι το μέσον της
είναι το μέσον της  και το
και το  ώστε
ώστε 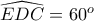
 ώστε
ώστε  , ενώ
, ενώ  είναι το μέσον της
είναι το μέσον της  . Να δειχθεί ότι η
. Να δειχθεί ότι η  είναι διχοτόμος της
είναι διχοτόμος της  Με
Με  η
η  είναι η μεσοκάθετος των
είναι η μεσοκάθετος των  και
και  οπότε το
οπότε το  είναι ισόπλευρο (αφού
είναι ισόπλευρο (αφού 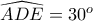 )
)  των
των  είναι συμμετρικά ως προς την
είναι συμμετρικά ως προς την  .
.  το κέντρο του
το κέντρο του  , τότε το
, τότε το  είναι εγγράψιμο σε κύκλο , ο οποίος τέμνει την
είναι εγγράψιμο σε κύκλο , ο οποίος τέμνει την  στο
στο  .
.  είναι συνευθειακά.
είναι συνευθειακά. που ισχύει αφού από το λήμμα
που ισχύει αφού από το λήμμα  ,άρα
,άρα 
ΗΓιώργος Μήτσιος έγραψε: ↑Κυρ Οκτ 30, 2022 10:27 pm
Σε τρίγωνομε
, το
είναι το μέσον της
και το
ώστε
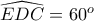
Ακόμη τοώστε
, ενώ
είναι το μέσον της
. Να δειχθεί ότι η
είναι διχοτόμος της
 τέμνει την
τέμνει την  στο
στο  . Με το Θ. Μενελάου , πρώτα στο τρίγωνο
. Με το Θ. Μενελάου , πρώτα στο τρίγωνο  και διατέμνουσα
και διατέμνουσα  προκύπτει
προκύπτει 
 με διατέμνουσα
με διατέμνουσα  παίρνουμε
παίρνουμε 
 οι διχοτόμοι των
οι διχοτόμοι των  και
και  τότε
τότε  , ενώ στο ισόπλευρο
, ενώ στο ισόπλευρο  είναι
είναι  .
. τότε και
τότε και  . Έτσι με τα Θ. Θαλή και διχοτόμου έχουμε:
. Έτσι με τα Θ. Θαλή και διχοτόμου έχουμε: , ΑΤΟΠΟ.
, ΑΤΟΠΟ. , συνεπώς
, συνεπώς  και
και  διχοτόμος της
διχοτόμος της .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες