Σελίδα 1 από 1
Από Σερβία ο λόγος
Δημοσιεύτηκε: Δευ Ιουν 27, 2022 11:28 am
από george visvikis
- Από Σερβία ο λόγος.png (14.22 KiB) Προβλήθηκε 1144 φορές
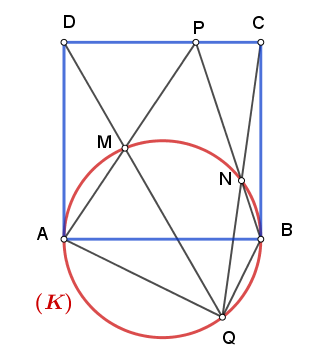
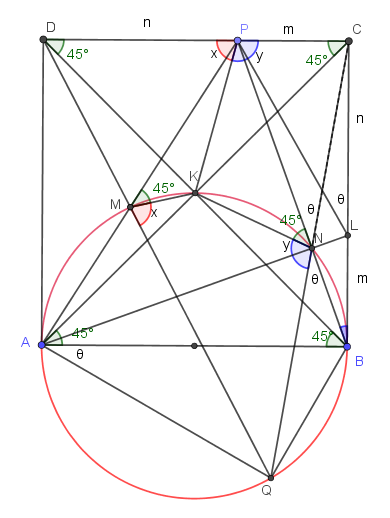
Δίνεται τετράγωνο

και ο κύκλος

διαμέτρου

Ένα σημείο

κινείται στην πλευρά

και οι

επανατέμνουν τον κύκλο στα

αντίστοιχα. Να δείξετε ότι οι

τέμνονται
σε σημείο

του

και ότι
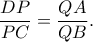
Re: Από Σερβία ο λόγος
Δημοσιεύτηκε: Δευ Ιουν 27, 2022 2:03 pm
από Ορέστης Λιγνός
george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 am
Από Σερβία ο λόγος.png
Δίνεται τετράγωνο

και ο κύκλος

διαμέτρου

Ένα σημείο

κινείται στην πλευρά

και οι

επανατέμνουν τον κύκλο στα

αντίστοιχα. Να δείξετε ότι οι

τέμνονται
σε σημείο

του

και ότι
Πολύ καλή κ. Γιώργο!

Έστω ότι οι διαγώνιοι

τέμνονται στο

.
Ισχυρισμός 1: Τα τετράπλευρα

και

είναι εγγράψιμα, έστω στους κύκλους
.
Απόδειξη: Προφανώς

, οπότε είναι

συνεπώς το τετράπλευρο

είναι εγγράψιμο. Όμοια και το τετράπλευρο

είναι εγγράψιμο

Στο πρόβλημα, είναι

άρα αν η

τέμνει τον

στο

, τότε

δηλαδή

, οπότε το πρώτο ερώτημα αποδείχθηκε.
Για το δεύτερο ερώτημα, χρειαζόμαστε έναν ακόμα Ισχυρισμό:
Ισχυρισμός 2: Οι ακτίνες των κύκλων
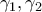
είναι ίσες.
Απόδειξη: Είναι, (

η ακτίνα του κύκλου

, με

)

οπότε

, όπως θέλαμε

Στο πρόβλημα, είναι

άρα

που αποδεικνύει το ζητούμενο.
Re: Από Σερβία ο λόγος
Δημοσιεύτηκε: Δευ Ιουν 27, 2022 6:33 pm
από george visvikis
Ορέστης Λιγνός έγραψε: ↑Δευ Ιουν 27, 2022 2:03 pm
george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 am
Από Σερβία ο λόγος.png
Δίνεται τετράγωνο

και ο κύκλος

διαμέτρου

Ένα σημείο

κινείται στην πλευρά

και οι

επανατέμνουν τον κύκλο στα

αντίστοιχα. Να δείξετε ότι οι

τέμνονται
σε σημείο

του

και ότι
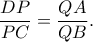
Πολύ καλή κ. Γιώργο!

Έστω ότι οι διαγώνιοι

τέμνονται στο

.
Ισχυρισμός 1: Τα τετράπλευρα

και

είναι εγγράψιμα, έστω στους κύκλους
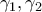
.
Απόδειξη: Προφανώς

, οπότε είναι

συνεπώς το τετράπλευρο

είναι εγγράψιμο. Όμοια και το τετράπλευρο

είναι εγγράψιμο

Στο πρόβλημα, είναι

άρα αν η

τέμνει τον

στο

, τότε

δηλαδή

, οπότε το πρώτο ερώτημα αποδείχθηκε.
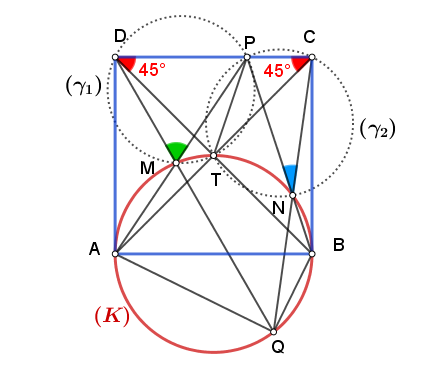
- Από Σερβία ο λόγος.II.png (23.09 KiB) Προβλήθηκε 1054 φορές
Για το δεύτερο ερώτημα, χρειαζόμαστε έναν ακόμα Ισχυρισμό:
Ισχυρισμός 2: Οι ακτίνες των κύκλων
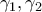
είναι ίσες.
Απόδειξη: Είναι, (

η ακτίνα του κύκλου

, με

)

οπότε

, όπως θέλαμε

Στο πρόβλημα, είναι

άρα

που αποδεικνύει το ζητούμενο.
To σχήμα στην πολύ ωραία λύση  του Ορέστη
του Ορέστη
Re: Από Σερβία ο λόγος
Δημοσιεύτηκε: Τετ Ιουν 29, 2022 12:07 am
από S.E.Louridas
george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 am
Από Σερβία ο λόγος.png
Δίνεται τετράγωνο

και ο κύκλος

διαμέτρου

Ένα σημείο

κινείται στην πλευρά

και οι

επανατέμνουν τον κύκλο στα

αντίστοιχα. Να δείξετε ότι οι

τέμνονται
σε σημείο

του

και ότι
Έπεσα πάνω στο ωραίο αυτό θέμα και μετά από την πολύ όμορφη λύση του Άριστου Ορέστη, ας δούμε και την διαπραγμάτευση που ακολουθεί και μόνο για λόγους μαθηματικής πολυφωνίας.
Αν

η άλλη τομή της

με τον κύκλο εκτός του σημείου

έχουμε:

Όμως από το εγγράψιμο

προκύπτει

Από τις

έχουμε ότι το σημείο

θα είναι σημείο της ευθείας

δηλαδή

και έτσι αποδείχτηκε το πρώτο ερώτημα.
Για το δεύτερο ερώτημα από τη προφανή ισότητα των ορθογωνίων τριγώνων

παίρνουμε

με τα ορθογώνια τρίγωνα

να προκύπτουν όμοια, αφού ισχύει

Συνεπώς τελικά έχουμε:

ή

- ΓΕΩ.png (111.44 KiB) Προβλήθηκε 953 φορές
Re: Από Σερβία ο λόγος
Δημοσιεύτηκε: Τετ Ιουν 29, 2022 11:12 am
από george visvikis
Αφού ευχαριστήσω και τον Σωτήρη για την επίσης πολύ ωραία λύση  ,
,
να δώσω και την πηγή της άσκησης: TST Serbia 2004.
edit: Διόρθωσα την χρονολογία στην πηγή.
Re: Από Σερβία ο λόγος
Δημοσιεύτηκε: Πέμ Ιουν 30, 2022 2:15 am
από Μιχάλης Τσουρακάκης
george visvikis έγραψε: ↑Δευ Ιουν 27, 2022 11:28 am
Από Σερβία ο λόγος.png
Δίνεται τετράγωνο

και ο κύκλος

διαμέτρου

Ένα σημείο

κινείται στην πλευρά

και οι

επανατέμνουν τον κύκλο στα

αντίστοιχα. Να δείξετε ότι οι

τέμνονται
σε σημείο

του

και ότι
Α)Λίγο διαφορετικά από τον
Ορέστη
Αν

το κέντρο του τετραγώνου,λόγω των γωνιών

τα

είναι εγράψιμμα,συνεπώς
οι μπλε γωνίες είναι ίσες όπως και οι κόκκινες
Αλλά

εγγράψιμμο, που αποδεικνύει το ζητούμενο
Β)Επειδή

οπότε και

Από τα ορθογώνια τρίγωνα

- Σέρβικη.png (33.53 KiB) Προβλήθηκε 885 φορές
 και ο κύκλος
και ο κύκλος  διαμέτρου
διαμέτρου  Ένα σημείο
Ένα σημείο  κινείται στην πλευρά
κινείται στην πλευρά 
 επανατέμνουν τον κύκλο στα
επανατέμνουν τον κύκλο στα  αντίστοιχα. Να δείξετε ότι οι
αντίστοιχα. Να δείξετε ότι οι  τέμνονται
τέμνονται  του
του  και ότι
και ότι 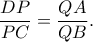
 και ο κύκλος
και ο κύκλος  διαμέτρου
διαμέτρου  Ένα σημείο
Ένα σημείο  κινείται στην πλευρά
κινείται στην πλευρά 
 επανατέμνουν τον κύκλο στα
επανατέμνουν τον κύκλο στα  αντίστοιχα. Να δείξετε ότι οι
αντίστοιχα. Να δείξετε ότι οι  τέμνονται
τέμνονται  του
του  και ότι
και ότι 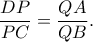
 τέμνονται στο
τέμνονται στο  .
. και
και  είναι εγγράψιμα, έστω στους κύκλους
είναι εγγράψιμα, έστω στους κύκλους  .
. , οπότε είναι
, οπότε είναι συνεπώς το τετράπλευρο
συνεπώς το τετράπλευρο 

 τέμνει τον
τέμνει τον  , τότε
, τότε 
 , οπότε το πρώτο ερώτημα αποδείχθηκε.
, οπότε το πρώτο ερώτημα αποδείχθηκε. η ακτίνα του κύκλου
η ακτίνα του κύκλου  , με
, με  )
)
 , όπως θέλαμε
, όπως θέλαμε 

 έχουμε:
έχουμε:  Όμως από το εγγράψιμο
Όμως από το εγγράψιμο  προκύπτει
προκύπτει  Από τις
Από τις  έχουμε ότι το σημείο
έχουμε ότι το σημείο  θα είναι σημείο της ευθείας
θα είναι σημείο της ευθείας  δηλαδή
δηλαδή  και έτσι αποδείχτηκε το πρώτο ερώτημα.
και έτσι αποδείχτηκε το πρώτο ερώτημα.  παίρνουμε
παίρνουμε 
 να προκύπτουν όμοια, αφού ισχύει
να προκύπτουν όμοια, αφού ισχύει 
 ή
ή  το κέντρο του τετραγώνου,λόγω των γωνιών
το κέντρο του τετραγώνου,λόγω των γωνιών  τα
τα  είναι εγράψιμμα,συνεπώς
είναι εγράψιμμα,συνεπώς εγγράψιμμο, που αποδεικνύει το ζητούμενο
εγγράψιμμο, που αποδεικνύει το ζητούμενο οπότε και
οπότε και 
