george visvikis έγραψε: ↑Σάβ Μάιος 21, 2022 10:58 am
Χρησιμοποιώντας το συμπέρασμα
αυτής της άσκησης (ή με οποιονδήποτε άλλο τρόπο) αποδείξτε την παρακάτω πρόταση:
Αν

είναι οι προβολές του σημείου Lemoine

τριγώνου

στις πλευρές του, τότε το

είναι το βαρύκεντρο του τριγώνου
 Επειδή είναι πιθανόν να έχει συζητηθεί ξανά, παρακαλώ μην δώσετε παραπομπές, μέχρι να γραφεί η πρώτη λύση. Ίσως υπάρχουν κάποιοι που την βλέπουν για πρώτη φορά.
Επειδή είναι πιθανόν να έχει συζητηθεί ξανά, παρακαλώ μην δώσετε παραπομπές, μέχρι να γραφεί η πρώτη λύση. Ίσως υπάρχουν κάποιοι που την βλέπουν για πρώτη φορά.
Καλημέρα Γιώργο!
Είναι γνωστή ιδιότητα του σημείου Lemoine τριγώνου (μια από τις πολλές χαρακτηριστικές του) αλλά ας δούμε μια απόδειξη (μάλλον πρωτοεμφανιζόμενη λόγω χρήσης νέου σχετικά θεωρήματος

)
Έστω
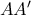
η
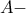
συμμετροδιάμεσος του τριγώνου

και ας είναι
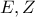
οι προβολές του σημείου
Lemoine L στις πλευρές

του

αντίστοιχα και
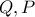
οι ορθές προβολές των
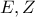
στις

αντίστοιχα. Προφανώς (από τα δύο ύψη) το
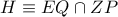
είναι το ορθόκεντρο του τριγώνου

, το τετράπλευρο

είναι εγγράψιμο σε κύκλο διαμέτρου

και το
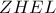
είναι παραλληλόγραμμο (απέναντι πλευρές παράλληλες λόγω καθετότητάς τους στην ίδια ευθεία) , οπότε

(το σημείο τομής των διαγωνίων του) είναι το μέσο (και) της

. Με

το ορθέκεντρο του


η ευθεία της διαμέσου

του

(αφού η διάμεσος και η συμμετροδιάμεσος από την ίδια κορυφή τριγώνου είναι ισογώνιες ως προς τις πλευρές της κορυφής αυτής).

- Βαρύκεντρο και αυτό.png (38.07 KiB) Προβλήθηκε 516 φορές
Αν

είναι οι ορθές προβολές του

στις

αντίστοιχα, τότε με

Όμως

(ορθογώνια με μια οξεία γωνία ίση) οπότε

και ομοίως από

Από

Από τη σχέση
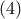
σύμφωνα με το
Stathis Koutras Theorem προκύπτει ότι

η ισοδύναμα η κάθετη από το σημείο Lemoine στην

διέρχεται από το μέσο της

. Κυκλικά προκύπτει ότι και οι εκ του

κάθετες στις

διέρχονται από τα μέσα των
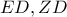
αντίστοιχα, άρα το

είναι το βαρύκεντρο του τριγώνου

και το ζητούμενο έχει αποδειχθεί .
Στάθης  είναι οι προβολές του σημείου Lemoine
είναι οι προβολές του σημείου Lemoine  τριγώνου
τριγώνου  στις πλευρές του, τότε το
στις πλευρές του, τότε το  είναι το βαρύκεντρο του τριγώνου
είναι το βαρύκεντρο του τριγώνου 

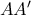 η
η 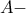 συμμετροδιάμεσος του τριγώνου
συμμετροδιάμεσος του τριγώνου  και ας είναι
και ας είναι 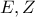 οι προβολές του σημείου
οι προβολές του σημείου  του
του 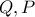 οι ορθές προβολές των
οι ορθές προβολές των  αντίστοιχα. Προφανώς (από τα δύο ύψη) το
αντίστοιχα. Προφανώς (από τα δύο ύψη) το 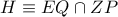 είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  , το τετράπλευρο
, το τετράπλευρο  είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  και το
και το 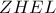 είναι παραλληλόγραμμο (απέναντι πλευρές παράλληλες λόγω καθετότητάς τους στην ίδια ευθεία) , οπότε
είναι παραλληλόγραμμο (απέναντι πλευρές παράλληλες λόγω καθετότητάς τους στην ίδια ευθεία) , οπότε  (το σημείο τομής των διαγωνίων του) είναι το μέσο (και) της
(το σημείο τομής των διαγωνίων του) είναι το μέσο (και) της  . Με
. Με  το ορθέκεντρο του
το ορθέκεντρο του 
 η ευθεία της διαμέσου
η ευθεία της διαμέσου  του
του  είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις
στις 
 (ορθογώνια με μια οξεία γωνία ίση) οπότε
(ορθογώνια με μια οξεία γωνία ίση) οπότε  και ομοίως από
και ομοίως από 

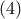 σύμφωνα με το
σύμφωνα με το  η ισοδύναμα η κάθετη από το σημείο Lemoine στην
η ισοδύναμα η κάθετη από το σημείο Lemoine στην  διέρχεται από το μέσο της
διέρχεται από το μέσο της  . Κυκλικά προκύπτει ότι και οι εκ του
. Κυκλικά προκύπτει ότι και οι εκ του 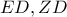 αντίστοιχα, άρα το
αντίστοιχα, άρα το  και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί . το σημείο τομής της εκ του
το σημείο τομής της εκ του  στην
στην  ανήκουν σε κύκλους διαμέτρων
ανήκουν σε κύκλους διαμέτρων  αντίστοιχα (λόγω των ορθών απέναντι γωνιών από κατασκευής).
αντίστοιχα (λόγω των ορθών απέναντι γωνιών από κατασκευής).
 και
και  και συνεπώς τα τρίγωνα
και συνεπώς τα τρίγωνα  είναι όμοια (δύο γωνίες ίσες μια προς μια) , άρα
είναι όμοια (δύο γωνίες ίσες μια προς μια) , άρα  , όπου
, όπου 
 και συνεπώς
και συνεπώς 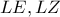 διέρχονται από τα μέσα
διέρχονται από τα μέσα  των
των  και συνεπώς το σημείο Lemoine του
και συνεπώς το σημείο Lemoine του  και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί .  είναι το σημείο τομής της εκ του σημείου Lemoine καθέτου
είναι το σημείο τομής της εκ του σημείου Lemoine καθέτου  , με
, με  το μέσο του ύψους
το μέσο του ύψους  . Από
. Από  και
και  , δηλαδή
, δηλαδή 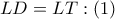
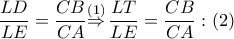 και με
και με 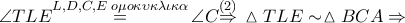
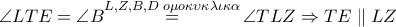
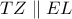 και συνεπώς το τετράπλευρο
και συνεπώς το τετράπλευρο  είναι παραλληλόγραμμο άρα η
είναι παραλληλόγραμμο άρα η  (δηλαδή η
(δηλαδή η  ) διέρχεται από το μέσο
) διέρχεται από το μέσο  της
της  το βαρύκεντρο του τριγώνου
το βαρύκεντρο του τριγώνου 
 έχουν (από το τετράπλευρο
έχουν (από το τετράπλευρο 
 και ομοίως προκύπτει ότι:
και ομοίως προκύπτει ότι: 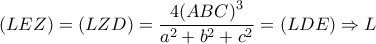 το βαρύκεντρο του
το βαρύκεντρο του  το συμμετρικό του
το συμμετρικό του  ως προς το μέσο
ως προς το μέσο  είναι παραλληλόγραμμο (οι διαγώνιές του διχοτομούνται) οπότε :
είναι παραλληλόγραμμο (οι διαγώνιές του διχοτομούνται) οπότε :  και
και 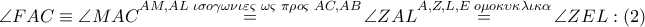
 και με
και με 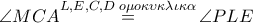 προκύπτει ότι τα
προκύπτει ότι τα  είναι ομόλογα τμήματα των ομοίων αυτών τριγώνων , και με
είναι ομόλογα τμήματα των ομοίων αυτών τριγώνων , και με 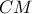 διάμεσο (από κατασκευής) του
διάμεσο (από κατασκευής) του 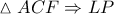 διάμεσος του
διάμεσος του  , δηλαδή η
, δηλαδή η  που χρησιμοποιήθηκε σε προηγούμενη απόδειξη
που χρησιμοποιήθηκε σε προηγούμενη απόδειξη