 η διχοτόμος τριγώνου
η διχοτόμος τριγώνου  με έγκεντρο
με έγκεντρο  και
και  το σημείο επαφής του εγγεγραμμένου κύκλου με την
το σημείο επαφής του εγγεγραμμένου κύκλου με την 
Έστω ακόμα
 σημείο του περιγεγραμμένου κύκλου ώστε
σημείο του περιγεγραμμένου κύκλου ώστε  Αν η
Αν η  τέμνει τον περίκυκλο του
τέμνει τον περίκυκλο του 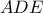 στο
στο να δείξετε ότι
να δείξετε ότι 
Συντονιστές: vittasko, silouan, rek2
 η διχοτόμος τριγώνου
η διχοτόμος τριγώνου  με έγκεντρο
με έγκεντρο  και
και  το σημείο επαφής του εγγεγραμμένου κύκλου με την
το σημείο επαφής του εγγεγραμμένου κύκλου με την 
 σημείο του περιγεγραμμένου κύκλου ώστε
σημείο του περιγεγραμμένου κύκλου ώστε  Αν η
Αν η  τέμνει τον περίκυκλο του
τέμνει τον περίκυκλο του 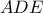 στο
στο να δείξετε ότι
να δείξετε ότι 
 ,
,  τα συμμετρικά των
τα συμμετρικά των  ,
,  ως προς το έγκεντρο
ως προς το έγκεντρο  αντίστοιχα. Αρκεί να αποδείξουμε ότι το τρίγωνο
αντίστοιχα. Αρκεί να αποδείξουμε ότι το τρίγωνο είναι ορθογώνιο στο
είναι ορθογώνιο στο  .
. τέμνει τη
τέμνει τη  στο σημείο
στο σημείο  που είναι το σημείο επαφής του
που είναι το σημείο επαφής του 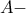 παρεγγεγραμμένου κύκλου με τη
παρεγγεγραμμένου κύκλου με τη  . Επομένως,
. Επομένως,  , οπότε και
, οπότε και  , όπου
, όπου  το μέσο
το μέσο . Εφόσον
. Εφόσον  , προκύπτει ότι οι ευθείες
, προκύπτει ότι οι ευθείες  ,
,  είναι συμμετρικές ως προς τη διάμετρο
είναι συμμετρικές ως προς τη διάμετρο 
 ,
,  τα μέσα των τόξων
τα μέσα των τόξων  ,
,  αντίστοιχα) του περιγεγραμμένου κύκλου του
αντίστοιχα) του περιγεγραμμένου κύκλου του  , επομένως το
, επομένως το  ανήκει στην διάμετρο
ανήκει στην διάμετρο  , και είναι το μέσο του
, και είναι το μέσο του  , οπότε
, οπότε 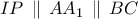 .
. έχουμε ότι
έχουμε ότι 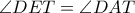 .
.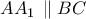 είναι
είναι  .
. είναι
είναι  .
.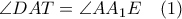 , και
, και  .
. το τετράπλευρο
το τετράπλευρο  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε 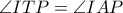 .
.  είναι παραλληλόγραμμο (οι διαγώνιοί του διχοτομούνται), τότε
είναι παραλληλόγραμμο (οι διαγώνιοί του διχοτομούνται), τότε  και
και  , δηλαδή, το τετράπλευρο
, δηλαδή, το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο. είναι ορθογώνιο στο
είναι ορθογώνιο στο  .
. .
. το συμμετρικό του
το συμμετρικό του  ως προς το έγκεντρο
ως προς το έγκεντρο  αντίστοιχα. Από γνωστό πρόβλημα η
αντίστοιχα. Από γνωστό πρόβλημα η  τέμνει τη
τέμνει τη 
 που είναι το σημείο επαφής του
που είναι το σημείο επαφής του 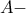 παρεγγεγραμμένου κύκλου με τη
παρεγγεγραμμένου κύκλου με τη  . Επομένως,
. Επομένως,  ,
,  , όπου
, όπου  το μέσο της
το μέσο της  . Εφόσον
. Εφόσον  , προκύπτει ότι οι ευθείες
, προκύπτει ότι οι ευθείες  ,
,  είναι συμμετρικές
είναι συμμετρικές  (
( ,
,  τα μέσα των τόξων
τα μέσα των τόξων  ,
,  αντίστοιχα) του περιγεγραμμένου κύκλου
αντίστοιχα) του περιγεγραμμένου κύκλου  του
του  ,
,  ανήκει στην διάμετρο
ανήκει στην διάμετρο  , και είναι το μέσο του
, και είναι το μέσο του  , οπότε
, οπότε 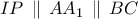 .
. έχουμε ότι
έχουμε ότι 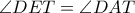 .
. είναι
είναι  .
. , δηλαδή το τετράπλευρο
, δηλαδή το τετράπλευρο 
 . Σε αυτόν τον κύκλο ανήκει και το μέσο
. Σε αυτόν τον κύκλο ανήκει και το μέσο  του τόξου
του τόξου  (που είναι και μέσο του τόξου
(που είναι και μέσο του τόξου  ) του κύκλου
) του κύκλου  , εφόσον
, εφόσον  .
. στον κύκλο
στον κύκλο  έχουμε
έχουμε  .
. (Λήμμα).
(Λήμμα).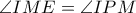 (το
(το  ορθογώνιο).
ορθογώνιο). , δηλαδή, το τρίγωνο
, δηλαδή, το τρίγωνο  είναι ισοσκελές,
είναι ισοσκελές,  .
. , (
, (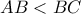 ),
),  το μέσο του τόξου
το μέσο του τόξου  του περιγεγραμμένου
του περιγεγραμμένου  ,
,  το έγκεντρο του
το έγκεντρο του 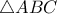 , και
, και  το μέσο της πλευράς
το μέσο της πλευράς  .
.  .
.
 επανατέμνει τον περιγεγραμμένο κύκλο στο
επανατέμνει τον περιγεγραμμένο κύκλο στο  τότε η
τότε η 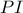
 του
του  προφανώς και του
προφανώς και του  Αν τώρα
Αν τώρα  είναι το αντιδιαμετρικό του
είναι το αντιδιαμετρικό του  τότε τα
τότε τα  είναι συνευθειακά.
είναι συνευθειακά.
 άρα το
άρα το  είναι εγγράψιμο. Οι
είναι εγγράψιμο. Οι  διέρχονται από τα σημεία
διέρχονται από τα σημεία  και
και  οπότε
οπότε  Αλλά η
Αλλά η  διχοτομεί την
διχοτομεί την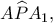 άρα είναι μεσοκάθετος της
άρα είναι μεσοκάθετος της  και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες