 είναι εγγεγραμμένο σε κύκλο διαμέτρου
είναι εγγεγραμμένο σε κύκλο διαμέτρου 
 προς το ίδιο μέρος της
προς το ίδιο μέρος της 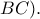 Αν
Αν  είναι
είναιη προβολή του
 στην
στην  να δείξετε ότι ο περίκυκλος του
να δείξετε ότι ο περίκυκλος του 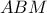 διέρχεται από το μέσο
διέρχεται από το μέσο  της χορδής
της χορδής 
Συντονιστές: vittasko, silouan, rek2
 είναι εγγεγραμμένο σε κύκλο διαμέτρου
είναι εγγεγραμμένο σε κύκλο διαμέτρου 
 προς το ίδιο μέρος της
προς το ίδιο μέρος της 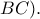 Αν
Αν  είναι
είναι στην
στην  να δείξετε ότι ο περίκυκλος του
να δείξετε ότι ο περίκυκλος του 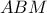 διέρχεται από το μέσο
διέρχεται από το μέσο  της χορδής
της χορδής 
Καλησπέρα κ. Γιώργο.george visvikis έγραψε: ↑Δευ Μαρ 21, 2022 10:49 amΤρίγωνοείναι εγγεγραμμένο σε κύκλο διαμέτρου

προς το ίδιο μέρος της
Αν
είναι
η προβολή τουστην
να δείξετε ότι ο περίκυκλος του
διέρχεται από το μέσο
της χορδής

 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  , και
, και  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Από το Θεώρημα της σπασμένης χορδής, είναι
. Από το Θεώρημα της σπασμένης χορδής, είναι  , οπότε
, οπότε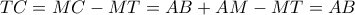
 και
και  έχουν
έχουν  ,
, 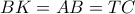 και
και  , συνεπώς είναι ίσα. Άρα,
, συνεπώς είναι ίσα. Άρα,  , δηλαδή
, δηλαδή
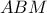 τέμενι την
τέμενι την  στο
στο  . Τότε,
. Τότε, 
 είναι ισοσκελές με
είναι ισοσκελές με  . Οπότε, τα
. Οπότε, τα  ανήκουν τόσο στην
ανήκουν τόσο στην  , όσο και στην μεσοκάθετο της
, όσο και στην μεσοκάθετο της  , οπότε πρέπει
, οπότε πρέπει  , που προφανώς δίνει το ζητούμενο.
, που προφανώς δίνει το ζητούμενο.Ας το δούμε και λιγάκι διαφορετικά από τον Ορέστη !george visvikis έγραψε: ↑Δευ Μαρ 21, 2022 10:49 amΑπό το μέσο της χορδής.png
Τρίγωνοείναι εγγεγραμμένο σε κύκλο διαμέτρου

προς το ίδιο μέρος της
Αν
είναι
η προβολή τουστην
να δείξετε ότι ο περίκυκλος του
διέρχεται από το μέσο
της χορδής

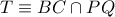 οπότε προφανώς με
οπότε προφανώς με  διάμετρο του περίκυκλου του τριγώνου
διάμετρο του περίκυκλου του τριγώνου  θα είναι
θα είναι  μεσοκάθετη της
μεσοκάθετη της  και ας είναι
και ας είναι  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  .
Τότε
.
Τότε  και προφανώς
και προφανώς  σημεία κύκλου διαμέτρου
σημεία κύκλου διαμέτρου  (λόγω των ορθών γωνιών
(λόγω των ορθών γωνιών 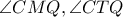 οπότε
οπότε 



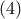 προκύπτει ότι
προκύπτει ότι  είναι ομόλογα τμήματα των ομοίων τριγώνων
είναι ομόλογα τμήματα των ομοίων τριγώνων 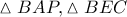 και με
και με  διάμεσο του
διάμεσο του  (από κατασκευής (λόγω της φερόμενης συμμετρίας)) θα είναι και
(από κατασκευής (λόγω της φερόμενης συμμετρίας)) θα είναι και  διάμεσος του
διάμεσος του  και το ζητούμενο έχει αποδειχθεί .
και το ζητούμενο έχει αποδειχθεί .Γράφω τον κύκλο που διέρχεται από ταgeorge visvikis έγραψε: ↑Δευ Μαρ 21, 2022 10:49 amΑπό το μέσο της χορδής.png
Τρίγωνοείναι εγγεγραμμένο σε κύκλο διαμέτρου

προς το ίδιο μέρος της
Αν
είναι
η προβολή τουστην
να δείξετε ότι ο περίκυκλος του
διέρχεται από το μέσο
της χορδής

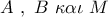 . Η
. Η  τον τέμνει ακόμα στο
τον τέμνει ακόμα στο  και δον αρχικό κύκλο στο
και δον αρχικό κύκλο στο  .
.  το σημείο τομής του κύκλου
το σημείο τομής του κύκλου  με τη χορδή
με τη χορδή  . Θα δείξω ότι το
. Θα δείξω ότι το  είναι μέσο του
είναι μέσο του  , δηλαδή ταυτίζεται με το
, δηλαδή ταυτίζεται με το  .
Επειδή
.
Επειδή  είναι ίσες το τετράπλευρο
είναι ίσες το τετράπλευρο  είναι ισοσκελές τραπέζιο και άρα ,
είναι ισοσκελές τραπέζιο και άρα ,  .
. έχει διάμετρο την
έχει διάμετρο την με άμεση συνέπεια το τετράπλευρο,
με άμεση συνέπεια το τετράπλευρο, 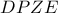 να είναι εγγράψιμο .
να είναι εγγράψιμο .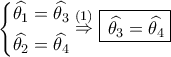
 είναι μεσοκάθετη στο
είναι μεσοκάθετη στο  και άρα το
και άρα το  είναι το μέσο της άλλης βάσης του ισοσκελούς τραπεζίου
είναι το μέσο της άλλης βάσης του ισοσκελούς τραπεζίου  .
.Ηgeorge visvikis έγραψε: ↑Δευ Μαρ 21, 2022 10:49 amΑπό το μέσο της χορδής.png
Τρίγωνοείναι εγγεγραμμένο σε κύκλο διαμέτρου

προς το ίδιο μέρος της
Αν
είναι
η προβολή τουστην
να δείξετε ότι ο περίκυκλος του
διέρχεται από το μέσο
της χορδής

 τέμνει τον κύκλο
τέμνει τον κύκλο  στο
στο  ,η
,η  τον τέμνει στο
τον τέμνει στο  ,η
,η  τέμνει τον κύκλο
τέμνει τον κύκλο στο
στο  και η
και η  τέμνει την
τέμνει την  στο
στο 
 κι επειδή το
κι επειδή το  προφανώς είναι ορθογώνιο,έχουμε
προφανώς είναι ορθογώνιο,έχουμε άρα
άρα 
 μεσοκάθετη της
μεσοκάθετη της 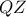 άρα και της
άρα και της 
 τα μέσα των
τα μέσα των 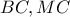 αντίστοιχα και
αντίστοιχα και  το σημείο τομής των
το σημείο τομής των  Θα δείξω ότι το σημείο
Θα δείξω ότι το σημείο  της
της  με το περίκυκλο του
με το περίκυκλο του 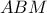 ταυτίζεται με το
ταυτίζεται με το  δηλαδή είναι το μέσο της χορδής
δηλαδή είναι το μέσο της χορδής 
 άρα
άρα 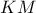 είναι η ευθεία Simson του τριγώνου
είναι η ευθεία Simson του τριγώνου  που αντιστοιχεί στο σημείο
που αντιστοιχεί στο σημείο 
 Επειδή η
Επειδή η  διχοτομεί την
διχοτομεί την  και το
και το  είναι εγγράψιμο, θα είναι
είναι εγγράψιμο, θα είναι  οπότε
οπότε  Όμως
Όμως  άρα οι πράσινες γωνίες είναι ίσες, όπως και οι κόκκινες. Τα τρίγωνα
άρα οι πράσινες γωνίες είναι ίσες, όπως και οι κόκκινες. Τα τρίγωνα 
 Αλλά
Αλλά  είναι το μέσο του
είναι το μέσο του  οπότε και το
οπότε και το  είναι μέσο του
είναι μέσο του 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες