 η διχοτόμος και
η διχοτόμος και  το έγκεντρο ισοσκελούς τριγώνου
το έγκεντρο ισοσκελούς τριγώνου  Η κάθετη από το
Η κάθετη από το  στην
στην  τέμνει
τέμνειτην
 στο
στο  και έστω
και έστω  το συμμετρικό του
το συμμετρικό του  ως προς την
ως προς την 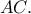 Να δείξετε ότι ο περίκυκλος του
Να δείξετε ότι ο περίκυκλος του 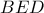 διέρχεται από το
διέρχεται από το 
Συντονιστές: vittasko, silouan, rek2
 η διχοτόμος και
η διχοτόμος και  το έγκεντρο ισοσκελούς τριγώνου
το έγκεντρο ισοσκελούς τριγώνου  Η κάθετη από το
Η κάθετη από το  στην
στην  τέμνει
τέμνει στο
στο  και έστω
και έστω  το συμμετρικό του
το συμμετρικό του  ως προς την
ως προς την 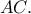 Να δείξετε ότι ο περίκυκλος του
Να δείξετε ότι ο περίκυκλος του 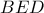 διέρχεται από το
διέρχεται από το 
 Έστω το σημείο
Έστω το σημείο  και ας είναι
και ας είναι  , το σημείο τομής του
, το σημείο τομής του  από την μεσοκάθετη ευθεία του τμήματος
από την μεσοκάθετη ευθεία του τμήματος  .
.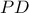 περνάει από το μέσον
περνάει από το μέσον  του τμήματος
του τμήματος  και έστω το σημείο
και έστω το σημείο  .
. και
και  προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι παραλληλόγραμμο και άρα
είναι παραλληλόγραμμο και άρα 
 τώρα, είναι ισοσκελές γιατί η μεσοκάθετη ευθεία της βάσης του
τώρα, είναι ισοσκελές γιατί η μεσοκάθετη ευθεία της βάσης του  , περνάει από το σημείο τομής
, περνάει από το σημείο τομής  των διαγωνίων του
των διαγωνίων του  και επομένως είναι εγγράψιμο.
και επομένως είναι εγγράψιμο. δηλαδή ανήκει στον περίκυκλο
δηλαδή ανήκει στον περίκυκλο  του τριγώνου
του τριγώνου  .
.
 Από
Από  και
και 
 οπότε το
οπότε το  είναι ισοσκελές τραπέζιο, λόγω
είναι ισοσκελές τραπέζιο, λόγω  και άρα εγγράψιμο.
και άρα εγγράψιμο. ανήκει στον περίκυκλο
ανήκει στον περίκυκλο  του τριγώνου
του τριγώνου  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. με
με  και έστω
και έστω  , το σημείο στην προέκταση της
, το σημείο στην προέκταση της  προς το μέρος του
προς το μέρος του  , ώστε να είναι
, ώστε να είναι  . Η δια του σημείου
. Η δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  , τέμνει την μεσοκάθετη ευθεία της πλευράς
, τέμνει την μεσοκάθετη ευθεία της πλευράς  στο σημείο έστω
στο σημείο έστω  και η μεσοκάθετη ευθεία του τμήματος
και η μεσοκάθετη ευθεία του τμήματος  τέμνει το
τέμνει το  στο σημείο έστω
στο σημείο έστω  . Αποδείξτε ότι η ευθεία
. Αποδείξτε ότι η ευθεία 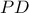 περνάει από το μέσον
περνάει από το μέσον  του τμήματος
του τμήματος  .
.vittasko έγραψε: ↑Κυρ Νοέμ 28, 2021 9:19 pmΛΗΜΜΑ. Δίνεται ισοσκελές τρίγωνομε
και έστω
, το σημείο στην προέκταση της
προς το μέρος του
, ώστε να είναι
. Η δια του σημείου
κάθετη ευθεία επί την
, τέμνει την μεσοκάθετη ευθεία της πλευράς
στο σημείο έστω
και η μεσοκάθετη ευθεία του τμήματος
τέμνει το
στο σημείο έστω
. Αποδείξτε ότι η ευθεία
περνάει από το μέσον
του τμήματος
.
 Έστω
Έστω  , ο κύκλος με κέντρο το σημείο
, ο κύκλος με κέντρο το σημείο  και ακτίνα
και ακτίνα  και έστω το σημείο
και έστω το σημείο  .
.
 και έστω το σημείο
και έστω το σημείο  .
. έχουμε ότι το σημείο
έχουμε ότι το σημείο  ανήκει στον κύκλο έστω
ανήκει στον κύκλο έστω  με διάμετρο το τμήμα
με διάμετρο το τμήμα  .
.
 Οι κύκλοι
Οι κύκλοι  τώρα, είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο
τώρα, είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο  και λόγο ομοιοθεσίας
και λόγο ομοιοθεσίας  και άρα, ισχύει
και άρα, ισχύει 


 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι παραλληλόγραμμο και άρα έχουμε
είναι παραλληλόγραμμο και άρα έχουμε 
 συμπεραίνεται ότι η ευθεία
συμπεραίνεται ότι η ευθεία 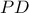 περνάει από το μέσον
περνάει από το μέσον  του τμήματος
του τμήματος  και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί. δεν μας χρειάζεται, αφού από
δεν μας χρειάζεται, αφού από 
 .
.Ας δούμε και μια διαφορετική αντιμετώπιση του προβλήματος Σύμφωνα με το Λήμμα που υπάρχει στην Διέλευση από το μέσο(δεν έδωσα πριν τη λύση στο παρόν γιατί βρήκα το εν λόγω λήμμα ενδιαφέρον και άλλωστε δεν θα παίρναμε τις καταπληκτικές λύσεις του (ιδιαίτερα του Μιχάλη (Τσουρακάκη)) ηgeorge visvikis έγραψε: ↑Τετ Νοέμ 24, 2021 11:47 amΟμοκυκλικά από συμμετρία.png
Έστωη διχοτόμος και
το έγκεντρο ισοσκελούς τριγώνου
Η κάθετη από το
στην
τέμνει
τηνστο
και έστω
το συμμετρικό του
ως προς την
Να δείξετε ότι ο περίκυκλος του
διέρχεται από το

 διέρχεται από το μέσο
διέρχεται από το μέσο  της
της  και ας είναι
και ας είναι  και
και  .
. (παράλληλες πλευρές του ίδιου προσανατολισμού) και με
(παράλληλες πλευρές του ίδιου προσανατολισμού) και με 

 διχοτομεί την εξωτερική (ως κάθετη στην εσωτερική διχοτόμο) γωνία του ισοσκελούς τριγώνου
διχοτομεί την εξωτερική (ως κάθετη στην εσωτερική διχοτόμο) γωνία του ισοσκελούς τριγώνου  και συνεπώς
και συνεπώς 
 ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες