Έστω

, το σημείο τομής της πλευράς

του δοσμένου τριγώνου

, από τον κύκλο έστω

χορδής

όπου

είναι το μέσον της

, ο οποίος εφάπτεται της ευθείας

, με

τυχόν σημείο επί της ευθείας

, εφαπτομένης του περίκυκλου

του

.
Αρκεί ως ισοδύναμο ζητούμενο να αποδειχθεί ότι η ευθεία

, όπου

είναι το μέσον της

, εφάπτεται στον περίκυκλο έστω

του τριγώνου

.

Έστω το σημείο

και από
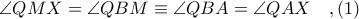
έχουμε ότι το τετράπλευρο
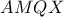
είναι εγγράψιμο σε κύκλο έστω

.
Έστω το σημείο

και έχουμε ότι το σημείο

ταυτίζεται με το
Σημείο Miquel στο πλήρες τετράπλευρο

και άρα, ο περίκυκλος του τριγώνου

περνάει από το σημείο

και επομένως, το σημείο

ανήκει στον κύκλο

.
Από

τώρα, προκύπτει ότι η ευθεία

εφάπτεται στον περίκυκλο έστω

του τριγώνου

.

- Τομή κύκλων σε ευθεία 2.
- f=181 t=70567.PNG (44.47 KiB) Προβλήθηκε 1421 φορές

Έστω το σημείο

και έχουμε ότι το τετράπλευρο

είναι τραπέζιο γιατί η ευθεία

περνάει από το μέσον έστω

του τμήματος

.
Σύμφωνα με το παρακάτω
Λήμμα, η εφαπτομένη του κύκλου

στο σημείο

, τέμνει τον περίκυκλο του τριγώνου

κατα το
Σημείο Miquel στο πλήρες τετράπλευρο

.
Το σημείο

δηλαδή, ταυτίζεται με το
Σημείο Miquel του

και άρα, το τετράπλευρο

είναι εγγράψιμο και επομένως ισχύει

Από
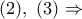

Από

συμπεραίνεται ότι η ευθεία

εφάπτεται του κύκλου

και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
ΛΗΜΜΑ. Δίνεται τραπέζιο  με
με  και έστω τα σημεία
και έστω τα σημεία  και
και  και ας είναι
και ας είναι  , το δεύτερο εκτός του
, το δεύτερο εκτός του  σημείο τομής των περικύκλων των τριγώνων
σημείο τομής των περικύκλων των τριγώνων  . Αποδείξτε ότι
. Αποδείξτε ότι 
.

Η απόδειξη αυτή αφιερώνεται σε ένδειξη τιμής, στον ταλαντούχο μαθητή
Ορέστη Λιγνό, που μας κάνει περήφανους με τις επιδόσεις του στα Μαθηματικά και τις επιτυχίες του στους διαγωνισμούς.
Κώστας Βήττας.
ΥΓ. Θα βάλω αργότερα την απόδειξη που έχω υπόψη μου για το ως άνω
Λήμμα.
 τα μέσα των πλευρών
τα μέσα των πλευρών  τριγώνου
τριγώνου  περιγεγραμμένου σε κύκλο
περιγεγραμμένου σε κύκλο  και ας είναι
και ας είναι  τυχόν σημείο της εφαπτόμενης του
τυχόν σημείο της εφαπτόμενης του  στο
στο  . Αν
. Αν  είναι οι κύκλοι που διέρχονται από τα
είναι οι κύκλοι που διέρχονται από τα  και
και  και εφάπτονται των
και εφάπτονται των  στα
στα  αντίστοιχα, να δειχθεί ότι το ένα από τα σημεία τομής τους (έστω
αντίστοιχα, να δειχθεί ότι το ένα από τα σημεία τομής τους (έστω όπως φαίνεται στο σχήμα) ανήκει στην
όπως φαίνεται στο σχήμα) ανήκει στην 

 χορδής
χορδής  όπου
όπου  είναι το μέσον της
είναι το μέσον της  , ο οποίος εφάπτεται της ευθείας
, ο οποίος εφάπτεται της ευθείας  , με
, με  , εφαπτομένης του περίκυκλου
, εφαπτομένης του περίκυκλου  του
του  , όπου
, όπου  είναι το μέσον της
είναι το μέσον της  , εφάπτεται στον περίκυκλο έστω
, εφάπτεται στον περίκυκλο έστω  του τριγώνου
του τριγώνου  .
. Έστω το σημείο
Έστω το σημείο  και από
και από 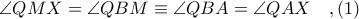 έχουμε ότι το τετράπλευρο
έχουμε ότι το τετράπλευρο 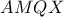 είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  .
. και έχουμε ότι το σημείο
και έχουμε ότι το σημείο  ταυτίζεται με το
ταυτίζεται με το  και άρα, ο περίκυκλος του τριγώνου
και άρα, ο περίκυκλος του τριγώνου  περνάει από το σημείο
περνάει από το σημείο  ανήκει στον κύκλο
ανήκει στον κύκλο  τώρα, προκύπτει ότι η ευθεία
τώρα, προκύπτει ότι η ευθεία  εφάπτεται στον περίκυκλο έστω
εφάπτεται στον περίκυκλο έστω  του τριγώνου
του τριγώνου  .
.
 και έχουμε ότι το τετράπλευρο
και έχουμε ότι το τετράπλευρο  είναι τραπέζιο γιατί η ευθεία
είναι τραπέζιο γιατί η ευθεία  περνάει από το μέσον έστω
περνάει από το μέσον έστω  του τμήματος
του τμήματος  .
. .
. είναι εγγράψιμο και επομένως ισχύει
είναι εγγράψιμο και επομένως ισχύει 
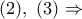

 συμπεραίνεται ότι η ευθεία
συμπεραίνεται ότι η ευθεία  με
με  και έστω τα σημεία
και έστω τα σημεία  και
και  και ας είναι
και ας είναι  σημείο τομής των περικύκλων των τριγώνων
σημείο τομής των περικύκλων των τριγώνων  . Αποδείξτε ότι
. Αποδείξτε ότι 
 έχουμε
έχουμε 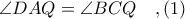 και
και 
 προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι όμοια και άρα, έχουμε
είναι όμοια και άρα, έχουμε 
 , οι προβολές του σημείου
, οι προβολές του σημείου  , αντιστοίχως.
, αντιστοίχως. έχουμε
έχουμε 
 και
και 

 προκύπτει ότι η ευθεία
προκύπτει ότι η ευθεία  ταυτίζεται με την
ταυτίζεται με την  .
. όμως, περνάει από τα μέσα
όμως, περνάει από τα μέσα  των βάσεων του δοσμένου τραπεζίου και άρα, ταυτίζεται με την
των βάσεων του δοσμένου τραπεζίου και άρα, ταυτίζεται με την 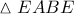 .
. και το
και το  λόγω του εγγραψίμου τετραπλεύρου
λόγω του εγγραψίμου τετραπλεύρου  και
και  λόγω της
λόγω της  , προκύπτει ότι η ευθεία
, προκύπτει ότι η ευθεία  εφάπτεται στον περίκυκλο του τριγώνου
εφάπτεται στον περίκυκλο του τριγώνου  και ομοίως, η ευθεία
και ομοίως, η ευθεία  εφάπτεται στον περίκυκλο του τριγώνου
εφάπτεται στον περίκυκλο του τριγώνου  .
. είναι η πολική του συμμετρικού του
είναι η πολική του συμμετρικού του  .
. 










 και
και  έπεται ότι
έπεται ότι  , όπως θέλαμε.
, όπως θέλαμε.