 τετράπλευρο
τετράπλευρο  , τα σημεία
, τα σημεία  και
και  είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  και
και  αντίστοιχα.
αντίστοιχα.Θεωρούμε επίσης τα σημεία
 ,
,  ,
,  ,
,  .
.Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνων
 και
και  εφάπτονται.
εφάπτονται.Συντονιστές: vittasko, silouan, rek2
 τετράπλευρο
τετράπλευρο  , τα σημεία
, τα σημεία  και
και  είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  και
και  αντίστοιχα.
αντίστοιχα. ,
,  ,
,  ,
,  .
. και
και  εφάπτονται.
εφάπτονται.Σημείωση : τηνgiannimani έγραψε: ↑Πέμ Οκτ 28, 2021 9:46 pmtang_cir.pngΣτο εγγεγραμμένο σε κύκλοτετράπλευρο
, τα σημεία
και
είναι τα μέσα των πλευρών
και
αντίστοιχα.
Θεωρούμε επίσης τα σημεία,
,
,
.
Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνωνκαι
εφάπτονται.
 δεν έπρεπε να την φερεις στο σχήμα γιατί " προδίδει " τη λύση
δεν έπρεπε να την φερεις στο σχήμα γιατί " προδίδει " τη λύση Έστωgiannimani έγραψε: ↑Πέμ Οκτ 28, 2021 9:46 pmtang_cir.pngΣτο εγγεγραμμένο σε κύκλοτετράπλευρο
, τα σημεία
και
είναι τα μέσα των πλευρών
και
αντίστοιχα.
Θεωρούμε επίσης τα σημεία,
,
,
.
Να αποδείξετε ότι οι περιγεγραμμένοι κύκλοι των τριγώνωνκαι
εφάπτονται.
 το σημείο Miquel του πλήρους τετραπλεύρου
το σημείο Miquel του πλήρους τετραπλεύρου  . Επειδή ο «κορμός» του
. Επειδή ο «κορμός» του  είναι τετράπλευρο εγγεγραμμένο στον κύκλο
είναι τετράπλευρο εγγεγραμμένο στον κύκλο  μια από τις ιδιότητές του εδώ είναι ότι
μια από τις ιδιότητές του εδώ είναι ότι  και
και  και επι πλέον από τις προφανείς καθετότητες (λόγω αποστημάτων)
και επι πλέον από τις προφανείς καθετότητες (λόγω αποστημάτων)  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  είναι σημεία κύκλου (έστω
είναι σημεία κύκλου (έστω  ) διαμέτρου
) διαμέτρου  και συνεπώς ο περίκυκλος του τριγώνου
και συνεπώς ο περίκυκλος του τριγώνου  διέρχεται (και) από το
διέρχεται (και) από το  .
.
 ομοκυκλικά άρα
ομοκυκλικά άρα 
 ομοκυκλικά άρα
ομοκυκλικά άρα 

 διέρχεται από το
διέρχεται από το  Οι περίκυκλοι λοιπόν των τριγώνων
Οι περίκυκλοι λοιπόν των τριγώνων  και
και  έχουν κοινό σημείο το
έχουν κοινό σημείο το  και επί πλέον
και επί πλέον 
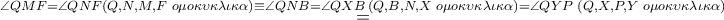

 και επειδή τα σημεία
και επειδή τα σημεία  είναι συνευθειακά προκύπτει ότι και τα σημεία
είναι συνευθειακά προκύπτει ότι και τα σημεία 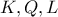 είναι συνευθειακά , άρα οι περίκυκλοι των τριγώνων
είναι συνευθειακά , άρα οι περίκυκλοι των τριγώνων  και
και  εφάπτονται ( έχουν κοινό σημείο που ανήκει στη διάκεντρό τους) και το ζητούμενο έχει αποδειχθεί .
εφάπτονται ( έχουν κοινό σημείο που ανήκει στη διάκεντρό τους) και το ζητούμενο έχει αποδειχθεί . ,
,  ,
,  και
και  .
. , έστω
, έστω 
 εφόσον τα σημεία
εφόσον τα σημεία  ,
,  ,
,  ,
,  είναι ομοκυκλικά.
είναι ομοκυκλικά. είναι το ζητούμενο σημείο επαφής.
είναι το ζητούμενο σημείο επαφής.  (σύνθεση στροφής με κέντρο το
(σύνθεση στροφής με κέντρο το  και γωνία
και γωνία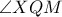 και ομοιοθεσίας με λόγο
και ομοιοθεσίας με λόγο 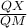 ) που στέλνει το
) που στέλνει το  στο
στο  και το
και το  στο
στο  , άρα μεταφέρει το τρίγωνο
, άρα μεταφέρει το τρίγωνο  στο τρίγωνο
στο τρίγωνο  .
. ,
,  ,
,  ,
,  είναι ομοκυκλικά.
είναι ομοκυκλικά. (από το εγγεγραμμένο
(από το εγγεγραμμένο  )
) (από το εγγράψιμο
(από το εγγράψιμο  )
) είναι εξωτερική της
είναι εξωτερική της 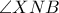 στο τρίγωνο
στο τρίγωνο  άρα
άρα 

 λαμβάνουμε:
λαμβάνουμε: 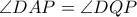
 και
και 
 και
και  είναι όμοια άρα
είναι όμοια άρα 
 είναι εγγράψιμο. Συνεπώς:
είναι εγγράψιμο. Συνεπώς: 
 , δηλαδή το
, δηλαδή το  ανήκει στον
ανήκει στον 
 ,
, ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά.  έχουμε:
έχουμε: 
 ισχύει
ισχύει  . Άρα
. Άρα 
 είναι εγγράψιμο.
είναι εγγράψιμο.  .
.  άρα
άρα 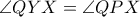
 ανήκει στον
ανήκει στον 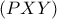
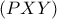 και
και  εφάπτονται στο
εφάπτονται στο  .
.
 και
και  .
. έχουμε
έχουμε 
 ,
,  ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά. 

 .
.
 ,
,  ,
,  ,
,  , και
, και 
 (Σημείο Miquel πέντε ευθειών). Αυτό προκύπτει από το επόμενο λήμμα:
(Σημείο Miquel πέντε ευθειών). Αυτό προκύπτει από το επόμενο λήμμα: και
και  κινούνται µε σταθερές ταχύτητες (όχι κατ' ανάγκη ίσες) σε δύο
κινούνται µε σταθερές ταχύτητες (όχι κατ' ανάγκη ίσες) σε δύο . Τότε, ο περιγεγραµµένος κύκλος
. Τότε, ο περιγεγραµµένος κύκλος  , διέρχεται από δύο σταθερά σηµεία
, διέρχεται από δύο σταθερά σηµεία  και
και  , όπου το
, όπου το  είναι
είναι  στα σηµεία
στα σηµεία  .
. και
και  που τέμνονται στο
που τέμνονται στο  . Αρχική θέση των σημείων
. Αρχική θέση των σημείων  και
και 
 και
και  αντίστοιχα. Μετά χρόνο
αντίστοιχα. Μετά χρόνο  , έστω ότι τα σημεία θα βρίσκονται στις θέσεις
, έστω ότι τα σημεία θα βρίσκονται στις θέσεις  και
και  αντίστοιχα,
αντίστοιχα,  θα βρίσκονται στις θέσεις
θα βρίσκονται στις θέσεις  και
και  (τα
(τα  και
και  μέσα των
μέσα των  και
και  ).
). ,
,  ,
,  ,
,  και για τις ευθείες
και για τις ευθείες  ,
,  ,
,  ,
,  είναι το ίδιο.
είναι το ίδιο. .
Εφόσον το τετράπλευρο
.
Εφόσον το τετράπλευρο  είναι εγγεγραμμένο στον κύκλο
είναι εγγεγραμμένο στον κύκλο  , σύμφωνα με γνωστές
, σύμφωνα με γνωστές  και
και  , και το σημείο τομής
, και το σημείο τομής 
 είναι το ορθόκεντρο του
είναι το ορθόκεντρο του 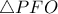 .
. ,
,  που θέλουμε να αποδείξουμε ότι εφάπτονται, είναι περιγεγραμμένοι κύκλοι
που θέλουμε να αποδείξουμε ότι εφάπτονται, είναι περιγεγραμμένοι κύκλοι . Θεωρούμε επίσης,
. Θεωρούμε επίσης,  του τριγώνου που σχηματίζουν οι ευθείες
του τριγώνου που σχηματίζουν οι ευθείες  ,
,  και
και  . Οι τρεις αυτές ευθείες είναι οι κοινές ευθείες των τετράδων
. Οι τρεις αυτές ευθείες είναι οι κοινές ευθείες των τετράδων  ,
,  ,
,  ,
, 
 ,
,  ,
,  σχηματίζουν το τρίγωνο
σχηματίζουν το τρίγωνο  ) και
) και  ,
,  ,
,  ,
,  (οι ευθείες
(οι ευθείες  ,
,  ,
, 
 )
) κέντρου
κέντρου  . Ο κύκλος αυτός διέρχεται προφανώς από το
. Ο κύκλος αυτός διέρχεται προφανώς από το  ,
, . Πράγματι, από τα ισοσκελή τρίγωνα
. Πράγματι, από τα ισοσκελή τρίγωνα 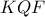 και
και 
 (από το ορθογώνιο τρίγωνο
(από το ορθογώνιο τρίγωνο  ).
). , οπότε η ακτίνα
, οπότε η ακτίνα  εφαπτομένη του κύκλου
εφαπτομένη του κύκλου  στο
στο  .
.  εφαπτομένη του και κύκλου
εφαπτομένη του και κύκλου  .
. (κατά κορυφήν)
(κατά κορυφήν)  (γωνία χορδή-εφαπτομένη)
(γωνία χορδή-εφαπτομένη)  (εγγεγραμμένες γωνίες στο ίδιο τόξο)
(εγγεγραμμένες γωνίες στο ίδιο τόξο)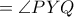 (εξωτερική ίση με την απέναντι εσωτερική σε εγγεγραμμένο τετράπλευρο), που αποδεικνύει τον τελευταίο ισχυρισμό.
(εξωτερική ίση με την απέναντι εσωτερική σε εγγεγραμμένο τετράπλευρο), που αποδεικνύει τον τελευταίο ισχυρισμό. ανήκει στην ευθεία
ανήκει στην ευθεία  προκύπτει
προκύπτει με τέμνουσα των πλευρών του την ευθεία
με τέμνουσα των πλευρών του την ευθεία  .
. ,
,  και
και  των τμημάτων
των τμημάτων  ,
,  και
και  αντίστοιχα, ανήκουν στην ίδια ευθεία.
αντίστοιχα, ανήκουν στην ίδια ευθεία.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες