 είναι το έγκεντρο και
είναι το έγκεντρο και  το βαρύκεντρο τριγώνου
το βαρύκεντρο τριγώνου  να βρείτε μία σχέση ανάμεσα
να βρείτε μία σχέση ανάμεσα στις πλευρές
 του τριγώνου, ώστε τα σημεία
του τριγώνου, ώστε τα σημεία  να είναι ομοκυκλικά.
να είναι ομοκυκλικά.Συντονιστές: vittasko, silouan, rek2
 είναι το έγκεντρο και
είναι το έγκεντρο και  το βαρύκεντρο τριγώνου
το βαρύκεντρο τριγώνου  να βρείτε μία σχέση ανάμεσα
να βρείτε μία σχέση ανάμεσα  του τριγώνου, ώστε τα σημεία
του τριγώνου, ώστε τα σημεία  να είναι ομοκυκλικά.
να είναι ομοκυκλικά.Ανgeorge visvikis έγραψε: ↑Τετ Οκτ 20, 2021 7:25 pmΑνείναι το έγκεντρο και
το βαρύκεντρο τριγώνου
να βρείτε μία σχέση ανάμεσα
στις πλευρέςτου τριγώνου, ώστε τα σημεία
να είναι ομοκυκλικά.
 ομοκυκλικά τότε
ομοκυκλικά τότε 
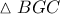 έχουμε:
έχουμε: 
![{{a}^{2}}=\dfrac{4}{9}\cdot \dfrac{2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}}+2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}}}{4}+\dfrac{8}{9}\cdot \dfrac{1}{4}\sqrt{\left[ 2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}} \right]\cdot \left[ 2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}} \right]}\cdot \sin \dfrac{A}{2} {{a}^{2}}=\dfrac{4}{9}\cdot \dfrac{2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}}+2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}}}{4}+\dfrac{8}{9}\cdot \dfrac{1}{4}\sqrt{\left[ 2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}} \right]\cdot \left[ 2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}} \right]}\cdot \sin \dfrac{A}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/1eeefe289fb614b7468b56314424d274.png) Από
Από  και έτσι η προηγούμενη σχέση γίνεται
και έτσι η προηγούμενη σχέση γίνεται![{{a}^{2}}=\dfrac{4}{9}\cdot \dfrac{2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}}+2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}}}{4}+\dfrac{1}{9}\sqrt{\dfrac{\left[ 2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}} \right]\cdot \left[ 2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}} \right]\cdot \left[ {{a}^{2}}-{{\left( b-c \right)}^{2}} \right]}{bc}} {{a}^{2}}=\dfrac{4}{9}\cdot \dfrac{2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}}+2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}}}{4}+\dfrac{1}{9}\sqrt{\dfrac{\left[ 2\left( {{a}^{2}}+{{c}^{2}} \right)-{{b}^{2}} \right]\cdot \left[ 2\left( {{a}^{2}}+{{b}^{2}} \right)-{{c}^{2}} \right]\cdot \left[ {{a}^{2}}-{{\left( b-c \right)}^{2}} \right]}{bc}}](/forum/ext/geomar/texintegr/latexrender/pictures/c267ee261f2ddb1b1c3e7860b0b65d9e.png)
 .
. όπου
όπου  το σημείο τομής της διχοτόμου της γωνίας
το σημείο τομής της διχοτόμου της γωνίας  του τριγώνου
του τριγώνου  με τον περίκυκλό του βάζω για διαπραγμάτευση την εξής κατασκευή.
Θεωρούμε χορδή
με τον περίκυκλό του βάζω για διαπραγμάτευση την εξής κατασκευή.
Θεωρούμε χορδή  κύκλου
κύκλου  και ας είναι
και ας είναι  ο κύκλος
ο κύκλος  με
με  το μέσο του ελάσσονος τόξου
το μέσο του ελάσσονος τόξου  .
. του
του  που βρίσκεται στο μέγιστο τόξο του
που βρίσκεται στο μέγιστο τόξο του  που ορίζεται από την
που ορίζεται από την  ώστε το σημείο
ώστε το σημείο  με
με  μεταξύ των
μεταξύ των  και το (μέσου)
και το (μέσου)  της
της  να είναι το βαρύκεντρο του τριγώνου
να είναι το βαρύκεντρο του τριγώνου 
Ισχύει ότι τα τρίγωναgeorge visvikis έγραψε: ↑Τετ Οκτ 20, 2021 7:25 pmΑνείναι το έγκεντρο και
το βαρύκεντρο τριγώνου
να βρείτε μία σχέση ανάμεσα
στις πλευρέςτου τριγώνου, ώστε τα σημεία
να είναι ομοκυκλικά.
 είναι όμοια άρα
είναι όμοια άρα 





Είναιgeorge visvikis έγραψε: ↑Τετ Οκτ 20, 2021 7:25 pmΑνείναι το έγκεντρο και
το βαρύκεντρο τριγώνου
να βρείτε μία σχέση ανάμεσα
στις πλευρέςτου τριγώνου, ώστε τα σημεία
να είναι ομοκυκλικά.


 άρα
άρα

 , θα δώσω μία προσέγγιση στην κατασκευή που προτείνει ο Στάθης.
, θα δώσω μία προσέγγιση στην κατασκευή που προτείνει ο Στάθης.O κύκλοςΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε: ↑Πέμ Οκτ 21, 2021 6:26 pm
Επειδή είναι πασίγνωστο ότι :όπου
το σημείο τομής της διχοτόμου της γωνίας
του τριγώνου
με τον περίκυκλό του βάζω για διαπραγμάτευση την εξής κατασκευή.
ενδειαφέρουσα κατασκευή.png
Θεωρούμε χορδήκύκλου
και ας είναι
ο κύκλος
με
το μέσο του ελάσσονος τόξου
.
Να κατασκευαστεί σημείο (σημεία)του
που βρίσκεται στο μέγιστο τόξο του
που ορίζεται από την
ώστε το σημείο
με
μεταξύ των
και το (μέσου)
της
να είναι το βαρύκεντρο του τριγώνου

 είναι γνωστός, καθώς και η χορδή
είναι γνωστός, καθώς και η χορδή  οπότε και η γωνία
οπότε και η γωνία  θα είναι γνωστή και έστω
θα είναι γνωστή και έστω  Θεωρείται γνωστό ότι το έγκεντρο
Θεωρείται γνωστό ότι το έγκεντρο  του τριγώνου
του τριγώνου  είναι σημείο του κύκλου
είναι σημείο του κύκλου  Επειδή όμως και το
Επειδή όμως και το  είναι σημείο του ίδιου κύκλου, θα είναι (σύμφωνα με την αρχική άσκηση)
είναι σημείο του ίδιου κύκλου, θα είναι (σύμφωνα με την αρχική άσκηση) 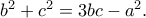

 (που είναι κατασκευάσιμο τμήμα).
(που είναι κατασκευάσιμο τμήμα). σε απόσταση
σε απόσταση  τέμνει τον κύκλο
τέμνει τον κύκλο  στην τρίτη κορυφή
στην τρίτη κορυφή  του ζητούμενου τριγώνου
του ζητούμενου τριγώνου 
 ο περίκυκλος του τριγώνου και
ο περίκυκλος του τριγώνου και  ο κύκλος που διέρχεται από τα σημεία
ο κύκλος που διέρχεται από τα σημεία 
 Επειδή όμως το
Επειδή όμως το  είναι σημείο του κύκλου
είναι σημείο του κύκλου  θα είναι
θα είναι  και
και  απ' όπου
απ' όπου 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες