Θα χρησιμοποιήσουμε την παρακάτω κατασκευή (Caratheodory, Theory of functions of a complex variable) καθώς την επεξήγηση που την συνοδεύει, για την εικόνα της ρίζας ενός μιγαδικού αριθμού, ως λήμμα.
Αν μας δίνετε το μοναδιαίο τμήμα

στο μιγαδικό επίπεδο και ένας μιγαδικός

σε αυτό τότε η εικόνα του μιγαδικού

δίνεται από την τομή του τμήματος

με το κύκλο

, όπου

το μέσο του τόξου

του περιγεγραμμένου κύκλου του τριγώνου

και

το αντιδιαμετρικό του

ως προς αυτόν το κύκλο.

- Screen Shot 2021-10-20 at 22.57.02.png (113.71 KiB) Προβλήθηκε 614 φορές
Στο προβλημά μας τώρα, εφαρμόζουμε το παραπάνω λήμμα με το μοναδιαίο τμήμα να αντιστοιχεί στην περίπτωσή μας στο

και ο μιγαδικός

στο σημείο

.
Άρα θα έχουμε

, σχέση δηλαδή επίκεντρης εγγεγραμμένης γωνίας. Επομένως

. Άρα το τρίγωνο

είναι ισοσκελές.
Ομοίως,

, σχέση επέκεντρης εγγεγραμμένης γωνίας. Επομένως

. Άρα και το τρίγωνο

είναι ισοσκελές.
Εν τέλη, παρατηρούμε ότι


.
Άρα το σημείο

ανήκει στην πλευρά

.

- summetriko_shmeio_tomhs_duo_kuklwn.png (40.72 KiB) Προβλήθηκε 614 φορές
 , που διέρχεται από την κορυφή
, που διέρχεται από την κορυφή  και το κέντρο
και το κέντρο  του περιγεγραμμένου κύκλου
του περιγεγραμμένου κύκλου , τέμνει τις πλευρές
, τέμνει τις πλευρές  ,
,  και τον περιγεγραμμένο κύκλο στα σημεία
και τον περιγεγραμμένο κύκλο στα σημεία ,
,  και
και  αντίστοιχα. Να αποδείξετε ότι το συμμετρικό του σημείου
αντίστοιχα. Να αποδείξετε ότι το συμμετρικό του σημείου  ως προς την ευθεία
ως προς την ευθεία  ,
, .
.
 το σημείο τομής της εκ του
το σημείο τομής της εκ του  . Τότε από
. Τότε από  και
και  προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι όμοια και με
είναι όμοια και με  προκύπτει ότι το τρίγωνο
προκύπτει ότι το τρίγωνο  είναι ισοσκελές (εξωτερική ίση με διπλάσια μιας απέναντι εσωτερικής) και συνεπώς και το τρίγωνο
είναι ισοσκελές (εξωτερική ίση με διπλάσια μιας απέναντι εσωτερικής) και συνεπώς και το τρίγωνο  (όμοιο του
(όμοιο του  ) είναι ισοσκελές , άρα
) είναι ισοσκελές , άρα  .
.
 «χαρταετός» και συνεπώς
«χαρταετός» και συνεπώς  μεσοκάθετη της
μεσοκάθετη της 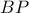 και
και 


 (ως άθροισμα (ή διαφορά) ανάλογα το σχήμα ίσων γωνιών)
(ως άθροισμα (ή διαφορά) ανάλογα το σχήμα ίσων γωνιών)

 σημείο του κύκλου
σημείο του κύκλου  μεσοκάθετη της
μεσοκάθετη της  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. τον περιγεγραμμένο κύκλο του
τον περιγεγραμμένο κύκλο του  . Έστω
. Έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  και
και  .
. προκύπτει ότι
προκύπτει ότι  , οπότε και
, οπότε και  ,
, . Όμοια,
. Όμοια,  .
. το συμμετρικό του
το συμμετρικό του  και
και  (λόγω των (1) και (2) ).
(λόγω των (1) και (2) ). και
και  είναι ισοσκελή με κορυφές τα
είναι ισοσκελή με κορυφές τα  και
και  .
. και
και  έχουμε
έχουμε  και
και  , και με πρόσθεση κατά μέλη (για την περίπτωση του σχήματος)
, και με πρόσθεση κατά μέλη (για την περίπτωση του σχήματος) . Αλλά, από το εγγεγραμμένο τετράπλευρο
. Αλλά, από το εγγεγραμμένο τετράπλευρο  στον κύκλο
στον κύκλο  .
. , δηλαδή,
, δηλαδή,  ,
,  τέµνονται στα σηµεία M, N, και η ευθεία
τέµνονται στα σηµεία M, N, και η ευθεία  διέρχεται από το M,
διέρχεται από το M, ,
,  αντίστοιχα. Έστω
αντίστοιχα. Έστω  ,
, 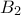 σημεία των
σημεία των  , αν και μόνο αν, τα σημεία
, αν και μόνο αν, τα σημεία  ,
,  .
. σε αυτό τότε η εικόνα του μιγαδικού
σε αυτό τότε η εικόνα του μιγαδικού  δίνεται από την τομή του τμήματος
δίνεται από την τομή του τμήματος  με το κύκλο
με το κύκλο  , όπου
, όπου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  και
και  το αντιδιαμετρικό του
το αντιδιαμετρικό του  και ο μιγαδικός
και ο μιγαδικός  , σχέση δηλαδή επίκεντρης εγγεγραμμένης γωνίας. Επομένως
, σχέση δηλαδή επίκεντρης εγγεγραμμένης γωνίας. Επομένως  . Άρα το τρίγωνο
. Άρα το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές. , σχέση επέκεντρης εγγεγραμμένης γωνίας. Επομένως
, σχέση επέκεντρης εγγεγραμμένης γωνίας. Επομένως  . Άρα και το τρίγωνο
. Άρα και το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.
 .
. ανήκει στην πλευρά
ανήκει στην πλευρά