(Συνέχεια ....)
Στο επόμενο σχήμα (Σχ. 4) θα δείξουμε ότι το κοινό σημείο

των κύκλων

και

είναι τελικά
και σημείο επαφής των κύκλων αυτών.

- Επαφή κύκλων 4.png (69.17 KiB) Προβλήθηκε 607 φορές
Στο σχήμα αυτό θεωρούμε τα αντίστροφα των κύκλων

και

ως προς πόλο την κορυφή

και
με κύκλο αντιστροφής τον κύκλο

.
Οι κύκλοι αυτοί είναι:
1ος) Ο κύκλος

ο οποίος ταυτίζεται με τον

διότι ο κύκλος

τέμνει ορθογώνια τον κύκλο αντιστροφής

.
Η λέξη βέβαια "ταυτίζεται" σημαίνει ότι ότι το αντίστροφο κάθε σημείου του κύκλου αυτού ανήκει στον ίδιο αυτό κύκλο.
2ος) Ο αντίστροφος

του κύκλου

, επειδή αυτός δεν διέρχεται από τον πόλο

, κατασκευάζεται ως ο ομοιόθετος αυτού,
δηλαδή του

, ως προς κέντρο ομοιοθεσίας τον πόλο αντιστροφής

και με λόγο ομοιοθεσίας:

όπου

η δύναμη αντιστροφής και

η δύναμη του πόλου αντιστροφής

ως προς τον κύκλο

.
Υπολογισμός των

.
Είναι:


Από τις (10) και (11) προκύπτει ο λόγος ομοιοθεσίας:

Σύμφωνα με τα ανωτέρω κατασκευάστηκαν οι κύκλοι

και

.
Στη συνέχεια αν θεωρήσουμε την ευθεία

η οποία είναι εφαπτομένη του κύκλου

στο σημείο

του ισοσκελούς τριγώνου

, τότε προφανώς κατά την ανωτέρω ομοιοθεσία, η εικόνα αυτής θα είναι η

,
η οριζομένη από την πλευρά

του τριγώνου αυτού.
Όμως κατά την ομοιοθεσία η επαφή δύο γραμμών διατηρείται. Έτσι η ευθεία

και ο κύκλος

ως ομοιόθετα
δυο γραμμών που εφάπτονται, θα είναι κι αυτά εφαπτόμενα και μάλιστα στο σημείο

.
Τελικά οι κύκλοι

εφάπτονται της

στο σημείο

και επειδή το αντίστροφο του σημείου

είναι το σημείο

, οι κύκλοι

και

εφάπτονται μεταξύ των στο σημείο

.
Κώστας Δόρτσιος
 . Θεωρούμε τον παρεγγεγραμμένο κύκλο
. Θεωρούμε τον παρεγγεγραμμένο κύκλο  που αντιστοιχεί στην κορυφή
που αντιστοιχεί στην κορυφή  , ο οποίος εφάπτεται των πλευρών
, ο οποίος εφάπτεται των πλευρών  στα σημεία
στα σημεία 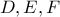 αντίστοιχα. Ο κύκλος
αντίστοιχα. Ο κύκλος  τέμνει τη
τέμνει τη  στα σημεία
στα σημεία  και
και  . Έστω ακόμη
. Έστω ακόμη  το μέσο της
το μέσο της  .Αποδείξτε ότι ο
.Αποδείξτε ότι ο  εφάπτεται του
εφάπτεται του  .
.
 , ο παρεγγεγραμμένος κύκλος
, ο παρεγγεγραμμένος κύκλος  στη γωνία
στη γωνία  και ο περιγεγραμμένος
και ο περιγεγραμμένος 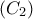 του τριγώνου
του τριγώνου  .
. το μέσο του τμήματος
το μέσο του τμήματος  , δηλαδή το κέντρο του κύκλου
, δηλαδή το κέντρο του κύκλου 
 είναι κάθετη στη χορδή
είναι κάθετη στη χορδή  και συνεπώς μεσοκάθετος αυτής. Άρα:
και συνεπώς μεσοκάθετος αυτής. Άρα: 
 είναι ισοσκελές.
είναι ισοσκελές. τμήσει τον κύκλο
τμήσει τον κύκλο  , τον διερχόμενο από τα σημεία
, τον διερχόμενο από τα σημεία  , στο σημείο
, στο σημείο  , τότε:
, τότε:
 , τότε, όμοια, θα είναι:
, τότε, όμοια, θα είναι:

 είναι το μέσο του
είναι το μέσο του 

 .
. τότε αυτή θα είναι προφανώς κάθετη στην
τότε αυτή θα είναι προφανώς κάθετη στην  θα είναι ισοσκελές. Άρα:
θα είναι ισοσκελές. Άρα: 
 η ακτίνα του παρεγγεγραμμένου κύκλου του τριγώνου
η ακτίνα του παρεγγεγραμμένου κύκλου του τριγώνου  και
και  .
.  ο οποίος ταυτίζεται με τον
ο οποίος ταυτίζεται με τον  του κύκλου
του κύκλου 
 η δύναμη αντιστροφής και
η δύναμη αντιστροφής και  η δύναμη του πόλου αντιστροφής
η δύναμη του πόλου αντιστροφής  .
.


 και
και  η οποία είναι εφαπτομένη του κύκλου
η οποία είναι εφαπτομένη του κύκλου  , τότε προφανώς κατά την ανωτέρω ομοιοθεσία, η εικόνα αυτής θα είναι η
, τότε προφανώς κατά την ανωτέρω ομοιοθεσία, η εικόνα αυτής θα είναι η  ,
, .
.  εφάπτονται της
εφάπτονται της