Μικτοεγγεγραμμένος και σταθερό σημείο

[george visvikis]

Μικτοεγγεγραμμένος και σταθερό σημείο.png (19.48 KiB) Προβλήθηκε 875 φορές

Τρίγωνο είναι εγγεγραμμένο σε κύκλο και είναι μεταβλητό σημείο της πλευράς Γράφουμε

τον κύκλο που εφάπτεται στα τμήματα στα σημεία αντίστοιχα και εσωτερικά στον κύκλο

Να δείξετε ότι η ευθεία διέρχεται από σταθερό σημείο.

[MAnTH05]

Έστω ότι η ευθεία τέμνει τη διχοτόμο της γωνίας στο σημείο . Θα αποδείξουμε ότι το ταυτίζεται με το έγκεντρο του (που είναι σταθερό). Αν , τότε ισχύει όπου το -παράκεντρο του .

Λήμμα
Τα σημεία είναι ομοκυκλικά.

Το κέντρο του είναι το μέσο του τόξου , δηλαδή το .

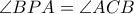Ακόμη, ισχύει (ως εγγεγραμμένες στο τόξο ) και (ως εγγεγραμμένες στο τόξο )

Έτσι:





Συνεπώςκαι το ζητούμενο έπεται.

λήμμα.png (54.2 KiB) Προβλήθηκε 623 φορές

[george visvikis]

Έστω ότι η ευθεία τέμνει τη διχοτόμο της γωνίας στο σημείο . Θα αποδείξουμε ότι το ταυτίζεται με το έγκεντρο του (που είναι σταθερό). Αν , τότε ισχύει όπου το -παράκεντρο του .

Λήμμα
Τα σημεία είναι ομοκυκλικά, (αφού το τετράπλευρο έχι δύο απέναντι ορθές γωνίες).

Από πού προκύπτει αυτό; (Θεωρείς ότι ισχύει αυτό που θέλεις να αποδείξεις).

[Doloros]

Μικτοεγγεγραμμένος και σταθερό σημείο.png
Τρίγωνο είναι εγγεγραμμένο σε κύκλο και είναι μεταβλητό σημείο της πλευράς Γράφουμε

τον κύκλο που εφάπτεται στα τμήματα στα σημεία αντίστοιχα και εσωτερικά στον κύκλο

Να δείξετε ότι η ευθεία διέρχεται από σταθερό σημείο.

Ας δούμε πρώτα μια κατασκευή του σχήματος .

Έστω λυμένο το πρόβλημα .

Μικτοεγγεγραμμένοσ και σταθερό σημείο_κατασκευή_1.png (37.95 KiB) Προβλήθηκε 649 φορές

Ο ομόκεντρος κύκλος που περνάει από το σταθερό σημείο του δεδομένου κύκλου θα εφάπτεται ,

σε σταθερή ευθεία παράλληλη στη διερχομένη από το και επί πλέον θα διέρχεται από το σημείο 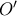, συμμετρικό του ως προς τη διχοτόμο της .

Δηλαδή έχουμε την κλασσική κατασκευή (1η Απολλώνια κατασκευή).

Αφού προσδιορίσουμε το κέντρο του κύκλου που θέλουμε , η απόστασή του από την ( ή την ) είναι η ακτίνα του.

[george visvikis]

Για την ιστορία, η πρόταση αυτή είναι γνωστή ως Λήμμα του Sawayama. Τρεις γνωστές

αποδείξεις είναι του Jean Louis Ayme του Jack D' Aurizio και του Oleg Golberg

[Al.Koutsouridis]

Να σημειώσουμε ότι το παραπάνω λήμμα ισχύει γενικότερα και για άλλες περιπτώσεις επαφής του μικτογεγγραμμένου κύκλου, όπως φαίνεται στα παρακάτω σχήματα. Η συσχέτιση με το θεώρημα Thébault είναι εμφανής.

lemma_Sawayama.png (156.66 KiB) Προβλήθηκε 538 φορές

Πηγή για τα σχήματα: περιοδικό Κβαντ, τεύχος 4, 2008.