Χρυσός και αυτός ;

Γιώργος Μήτσιος · #1

Καλησπέρα σε όλους!

: 31-1 Χρυσός λόγος.png (153.5 KiB) Προβλήθηκε 625 φορές

Το τρίγωνο ABC

έχει

. Θεωρούμε το $E \in BC$ ώστε να είναι $\widehat{AEC}=2\widehat{EAC}$ .

Στην προέκταση της

παίρνουμε

. Αν είναι $\widehat{BIA}=30^o$ τότε

Να εξεταστεί η σχέση του λόγου $\dfrac{\left ( ICA \right )}{(ABE)}$ με τον χρυσό αριθμό $\Phi$ . Σας ευχαριστώ, Γιώργος.

#2

Έστω τρίγωνο $ADI \to \left( {24^\circ ,126^\circ ,30^\circ } \right)$ . Γράφω τον κύκλο $\left( {A,AC} \right)$ και τέμνει , ακόμα, την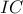

στο

. Θα είναι $\vartriangle ABC \to \left( {72^\circ ,54^\circ ,54^\circ } \right)$ .

Θεωρώ σημείο

της

για το οποίο $\widehat {BAE} = 30^\circ$ , έτσι $\widehat {CEI} = 42^\circ \,\,\kappa \alpha \iota \,\,\widehat {AEC} = 84^\circ$ δηλαδή η μια διπλάσια της άλλης .

Γράφω τον κύκλο A,B,C

και τέμνει την

στο

οπότε $\widehat {CDI} = 54^\circ$ .

Τα τρίγωνα $ABE\,\,\kappa \alpha \iota \,\,DIC$ είναι ισογώνια , ενώ $\widehat {ACD} = 30^\circ$ .

Γράφω και τον κύκλο D,C,I

στον οποίο εφάπτεται η

και αν

το κέντρο του θα είναι ισόπλευρο το $\vartriangle LDC$ .

Από το νόμο των ημιτόνων στα $\vartriangle DCI\,\,\kappa \alpha \iota \,\,DAC$ και την ομοιότητα :
$\vartriangle ACI \approx \vartriangle ADC$ έχω:

: Χρυσός κι αυτός_new.png (35.56 KiB) Προβλήθηκε 486 φορές

$\left\{ \begin{gathered} \frac{{IC}}{{DC}} = \frac{{\sin 54^\circ }}{{\sin 30^\circ }} = \varphi \hfill \\ \frac{{AC}}{{AD}} = \frac{{IC}}{{DC}} = \frac{{AI}}{{AC}} = \varphi \hfill \\ \end{gathered} \right.$

Επίσης : $\left\{ \begin{gathered} \frac{{DI}}{{DC}} = \frac{{\sin 96^\circ }}{{\sin 30^\circ }} \hfill \\ \frac{{DA}}{{DC}} = \frac{{\sin 30^\circ }}{{\sin 24^\circ }} \hfill \\ \end{gathered} \right. \Rightarrow \dfrac{{DI}}{{DA}} = 4\sin 96^\circ \sin 24^\circ = 2\left( {\cos 72^\circ - \cos 120^\circ } \right) = 2\cos 72^\circ + 1 = \varphi$

Από τα παραπάνω προκύπτει ότι DI = AC = AB

και έτσι : $\boxed{\frac{{\left( {ICA} \right)}}{{\left( {ABE} \right)}} = \frac{{IA \cdot IC}}{{AB \cdot AE}} = \frac{{IA}}{{AB}} = \frac{{IA}}{{DI}} = \varphi }$ .

Χρυσός και αυτός ;

Χρυσός και αυτός ;

Re: Χρυσός και αυτός ;

Μέλη σε σύνδεση