Στάθη σ' ευχαριστώ για την ( των "Βρυξελλών" ) λύση σου με διαφορετική προσέγγιση.

Ας δούμε και την λύση των "Αθηνών".

Έστω ότι έχει βρεθεί το ζητούμενο σημείο

και ισχύει

όπως ορίζεται στην εκφώνηση.
Έστω το σημείο

και στο τρίγωνο
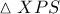
έχουμε ότι το σημείο έστω

, ταυτίζεται με την προβολή του σημείου

επί της

.

Γνωστό αποτέλεσμα, σύμφωνα με το οποίο και η προβολή του σημείου

επί της ευθείας
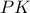
, έστω το σημείο

, ανήκει επίσης στην ευθεία

, όπου

είναι διχοτόμοι του
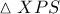

.
Ομοίως, θεωρούμε το τρίγωνο

και έχουμε ότι το ως ανω σημείο

, ανήκει επίσης στην ευθεία

, στην οποία ανήκει και το σημείο έστω

, ως η προβολή του σημείου

επί της ευθείας
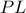
.
Άρα, για το μεταβλητό σημείο

εν γένει, προκύπτει ότι το σημείο
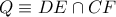
, κείται επί της

.

- Προσδιορισμός σημείου 5.
- f 181_t 68545a.PNG (53.04 KiB) Προβλήθηκε 598 φορές

Δια των σημείων

, φέρνουμε τις παράλληλες ευθείες προς τις ευθείες
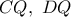
αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω

, κείμενο επί της ευθείας

, σύμφωνα με το παρακάτω γνωστό
Λήμμα, λόγω του τραπεζίου

ορθογωνίου εδώ αλλά και εν γένει


με

.
Έστω τα σημεία

και

.
Από τα όμοια ορθογώνια τρίγωνα

έχουμε

Από τα όμοια ορθογώνια τρίγωνα

έχουμε

Από
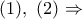


λόγω

.
Το σημείο

δηλαδή, ταυτίζεται με το μέσον του τμήματος

.
Επομένως, σύμφωνα πάλι με το
Λήμμα ( ειδική περίπτωση ), έχουμε ότι το σημείο
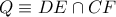
, ταυτίζεται με το σημείο τομής της

από την δια του σημείου έστω

παράλληλη ευθεία προς τις βάσεις του τραπεζίου ( εν γένει )

και άρα, είναι σταθερό σημείο.
Αποδεικνύεται έτσι, ότι και το ζητούμενο σημείο

είναι επίσης σταθερό, ως το σημείο του οποίου η προβολή επί της

ταυτίζεται με το σταθερό σημείο

και το ζητούμενο έχει βρεθεί.
ΛΗΜΜΑ. Δίνεται τραπέζιο  με
με  και έστω
και έστω  , τυχόν σημείο επί της πλευράς του
, τυχόν σημείο επί της πλευράς του  . Δια των σημείων
. Δια των σημείων  , φέρνουμε τις παράλληλες ευθείες προς τις ευθείες
, φέρνουμε τις παράλληλες ευθείες προς τις ευθείες  αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω
αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω  . Αποδείξτε ότι
. Αποδείξτε ότι 
.
Κώστας βήττας.
ΥΓ. Για την απόδειξη του ως άνω
Λήμματος, βρήκα αυτήν την
παραπομπή.
 κείμενοι εκτός αλλήλων και έστω
κείμενοι εκτός αλλήλων και έστω  , οι κοινές εξωτερικές εφαπτόμενες αυτών, με τα
, οι κοινές εξωτερικές εφαπτόμενες αυτών, με τα  σημεία έστω του κύκλου
σημεία έστω του κύκλου  . Έστω
. Έστω  , μεταβλητό σημείο μεταξύ των
, μεταβλητό σημείο μεταξύ των  και ας είναι
και ας είναι  , οι εφαπτόμενες των κύκλων
, οι εφαπτόμενες των κύκλων  , αντιστοίχως. Προσδιορίστε την θέση του σημείου
, αντιστοίχως. Προσδιορίστε την θέση του σημείου  ωστε να είναι
ωστε να είναι  , όπου
, όπου  και
και 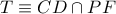 .
Κώστας Βήττας.
.
Κώστας Βήττας.
 Έστω ο περίκυκλος του τριγώνου
Έστω ο περίκυκλος του τριγώνου  , όπου
, όπου  το μέσο της
το μέσο της  και ας είναι
και ας είναι  το δεύτερο εκτός του
το δεύτερο εκτός του  αφού οι κύκλοι δεν είναι ίσοι.
αφού οι κύκλοι δεν είναι ίσοι. είναι όμοια (παράλληλες (ως κάθετες στις ίδιες ευθείες (τις κοινές εφαπτόμενες των κύκλων) τις ίσες πλευρές τους ) και συνεπώς
είναι όμοια (παράλληλες (ως κάθετες στις ίδιες ευθείες (τις κοινές εφαπτόμενες των κύκλων) τις ίσες πλευρές τους ) και συνεπώς  ισοσκελές τραπέζιο.
ισοσκελές τραπέζιο.  τότε είναι:
τότε είναι:  (
( μη κυρτή) και
μη κυρτή) και 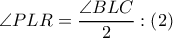 (
(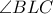 κυρτή). Αλλά από την ομοιότητα των ισοσκελών τριγώνων
κυρτή). Αλλά από την ομοιότητα των ισοσκελών τριγώνων  ( μη κυρτή – κυρτή ) οπότε από
( μη κυρτή – κυρτή ) οπότε από  ομοκυκλικά.
ομοκυκλικά.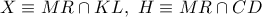 . Τότε από
. Τότε από 

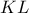 άξονας συμμετρίας του βασικού σχήματος (άρα και του ισοσκελούς τραπεζίου
άξονας συμμετρίας του βασικού σχήματος (άρα και του ισοσκελούς τραπεζίου  εγγράψιμο σε κύκλο και με
εγγράψιμο σε κύκλο και με  οπότε λόγω συμμετρίας το
οπότε λόγω συμμετρίας το  είναι το μέσο της
είναι το μέσο της  , δηλαδή
, δηλαδή 
 και επειδή
και επειδή  είναι το ύψος του τριγώνου
είναι το ύψος του τριγώνου  το σημείο
το σημείο 
 προκύπτει ότι τα ορθογώνια τρίγωνα
προκύπτει ότι τα ορθογώνια τρίγωνα  είναι όμοια οπότε
είναι όμοια οπότε 
 προκύπτει ότι
προκύπτει ότι 
 και συνεπώς το σημείο που προσδιορίστηκε ως το δεύτερο σημείο τομής (εκτός του μέσου
και συνεπώς το σημείο που προσδιορίστηκε ως το δεύτερο σημείο τομής (εκτός του μέσου  με την
με την  Έστω ότι έχει βρεθεί το ζητούμενο σημείο
Έστω ότι έχει βρεθεί το ζητούμενο σημείο  και ισχύει
και ισχύει  και στο τρίγωνο
και στο τρίγωνο 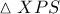 έχουμε ότι το σημείο έστω
έχουμε ότι το σημείο έστω  , ταυτίζεται με την προβολή του σημείου
, ταυτίζεται με την προβολή του σημείου  .
. Γνωστό αποτέλεσμα, σύμφωνα με το οποίο και η προβολή του σημείου
Γνωστό αποτέλεσμα, σύμφωνα με το οποίο και η προβολή του σημείου  επί της ευθείας
επί της ευθείας 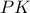 , έστω το σημείο
, έστω το σημείο  , ανήκει επίσης στην ευθεία
, ανήκει επίσης στην ευθεία  , όπου
, όπου  είναι διχοτόμοι του
είναι διχοτόμοι του  .
. και έχουμε ότι το ως ανω σημείο
και έχουμε ότι το ως ανω σημείο  , ανήκει επίσης στην ευθεία
, ανήκει επίσης στην ευθεία  , στην οποία ανήκει και το σημείο έστω
, στην οποία ανήκει και το σημείο έστω  , ως η προβολή του σημείου
, ως η προβολή του σημείου 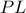 .
.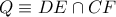 , κείται επί της
, κείται επί της  .
.
 , φέρνουμε τις παράλληλες ευθείες προς τις ευθείες
, φέρνουμε τις παράλληλες ευθείες προς τις ευθείες 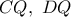 αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω
αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω  , κείμενο επί της ευθείας
, κείμενο επί της ευθείας  , σύμφωνα με το παρακάτω γνωστό
, σύμφωνα με το παρακάτω γνωστό  με
με  .
. και
και  .
. έχουμε
έχουμε 
 έχουμε
έχουμε 

 λόγω
λόγω  παράλληλη ευθεία προς τις βάσεις του τραπεζίου ( εν γένει )
παράλληλη ευθεία προς τις βάσεις του τραπεζίου ( εν γένει )  με
με  και έστω
και έστω  , τυχόν σημείο επί της πλευράς του
, τυχόν σημείο επί της πλευράς του  . Δια των σημείων
. Δια των σημείων  αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω
αντιστοίχως, οι οποίες τέμνονται στο σημείο έστω  . Αποδείξτε ότι
. Αποδείξτε ότι 