Σελίδα 1 από 1
Η τύχη του θεματοδότη
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 10:12 pm
από KARKAR

- Η τύχη του θεματοδότη.png (19.75 KiB) Προβλήθηκε 434 φορές
Σε κύκλο

είναι εγγεγραμμένο το ισοσκελές τρίγωνο

. Στο μικρό
τόξο

, κινείται σημείο

. Φέρουμε :
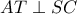
. α) Δείξτε ότι :

β) Αν

και ύψος

, υπολογίστε την μέγιστη τιμή του γινομένου

.
Re: Η τύχη του θεματοδότη
Δημοσιεύτηκε: Τετ Φεβ 12, 2020 11:48 pm
από Doloros
KARKAR έγραψε: ↑Τετ Φεβ 12, 2020 10:12 pm
Η τύχη του θεματοδότη.pngΣε κύκλο

είναι εγγεγραμμένο το ισοσκελές τρίγωνο

. Στο μικρό
τόξο

, κινείται σημείο

. Φέρουμε :
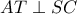
. α) Δείξτε ότι :

β) Αν

και ύψος

, υπολογίστε την μέγιστη τιμή του γινομένου

.
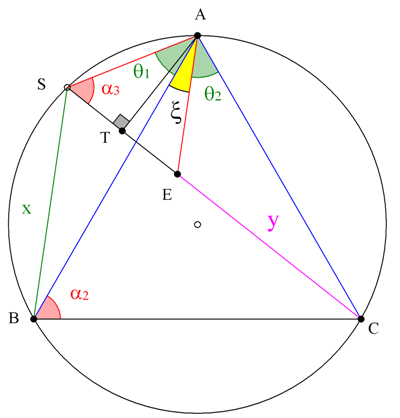
- Η τύχη του θεματοδότη_a.png (31.16 KiB) Προβλήθηκε 398 φορές
α) Αν

το συμμετρικό του

ως προς το

, τα ισοσκελή τρίγωνα

έχουν:

και άρα είναι ισογώνια οπότε :

.
Έτσι εύκολα έχουμε ότι

.
Μεταβλητό στην περίπτωση είναι το σημείο

.
Επειδή από την ομοιότητα των τριγώνων

( σταθερό ) και

(μεταβλητό) έχω:

- Η τύχη του θεματοδότη_b.png (35.86 KiB) Προβλήθηκε 378 φορές

.
Όπου

η απόσταση του

από τη σταθερή

(ή του

από την

) που γίνεται
μέγιστη αν το

ταυτιστεί με το μέσο του τόξου στο οποίο κινείται.
Ειδικά αν

υπολογίζονται :
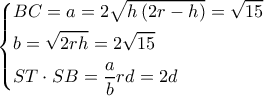
Αλλά η απόσταση του κέντρου από την

είναι:
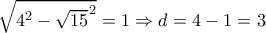
και άρα
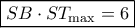
Re: Η τύχη του θεματοδότη
Δημοσιεύτηκε: Πέμ Φεβ 13, 2020 1:21 pm
από george visvikis
KARKAR έγραψε: ↑Τετ Φεβ 12, 2020 10:12 pm
Η τύχη του θεματοδότη.pngΣε κύκλο

είναι εγγεγραμμένο το ισοσκελές τρίγωνο

. Στο μικρό
τόξο

, κινείται σημείο

. Φέρουμε :
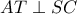
. α) Δείξτε ότι :

β) Αν

και ύψος

, υπολογίστε την μέγιστη τιμή του γινομένου

.
α) Πρόκειται για το
πρόβλημα της σπασμένης χορδής του Αρχμήδη.

- Η τύχη του KARKAR.png (15.34 KiB) Προβλήθηκε 337 φορές
β) Είναι

και εύκολα

Θέτω

Με νόμο συνημιτόνων στα τρίγωνα

παίρνω διαδοχικά
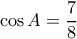
και



Άρα,

που παρουσιάζει για

μέγιστο ίσο με

(Εύκολα διαπιστώνουμε ότι σε αυτή τη θέση το

είναι μέσο του τόξου

).
 είναι εγγεγραμμένο το ισοσκελές τρίγωνο
είναι εγγεγραμμένο το ισοσκελές τρίγωνο  . Στο μικρό
. Στο μικρό  , κινείται σημείο
, κινείται σημείο  . Φέρουμε :
. Φέρουμε : 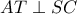 . α) Δείξτε ότι :
. α) Δείξτε ότι : 
 και ύψος
και ύψος  , υπολογίστε την μέγιστη τιμή του γινομένου
, υπολογίστε την μέγιστη τιμή του γινομένου  .
. είναι εγγεγραμμένο το ισοσκελές τρίγωνο
είναι εγγεγραμμένο το ισοσκελές τρίγωνο  . Στο μικρό
. Στο μικρό  , κινείται σημείο
, κινείται σημείο  . Φέρουμε :
. Φέρουμε : 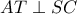 . α) Δείξτε ότι :
. α) Δείξτε ότι : 
 και ύψος
και ύψος  , υπολογίστε την μέγιστη τιμή του γινομένου
, υπολογίστε την μέγιστη τιμή του γινομένου  .
. το συμμετρικό του
το συμμετρικό του  , τα ισοσκελή τρίγωνα
, τα ισοσκελή τρίγωνα  έχουν:
έχουν:  και άρα είναι ισογώνια οπότε :
και άρα είναι ισογώνια οπότε :  .
. .
. ( σταθερό ) και
( σταθερό ) και  (μεταβλητό) έχω:
(μεταβλητό) έχω:  .
.  η απόσταση του
η απόσταση του  (ή του
(ή του  ) που γίνεται
) που γίνεται  υπολογίζονται :
υπολογίζονται :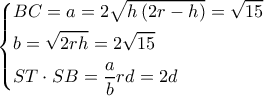
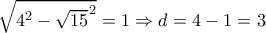
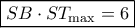
 και εύκολα
και εύκολα  Θέτω
Θέτω 
 παίρνω διαδοχικά
παίρνω διαδοχικά 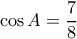 και
και 


 που παρουσιάζει για
που παρουσιάζει για  μέγιστο ίσο με
μέγιστο ίσο με  (Εύκολα διαπιστώνουμε ότι σε αυτή τη θέση το
(Εύκολα διαπιστώνουμε ότι σε αυτή τη θέση το  ).
).