 και οι διάμεσοί του
και οι διάμεσοί του  που τέμνονται στο
που τέμνονται στο  . Το σημείο
. Το σημείο  διατρέχει την πλευρά
διατρέχει την πλευρά  .
. Φέρουμε τις
 και
και  με
με 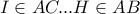 .
.Να εξεταστεί αν το
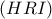 γίνεται μέγιστο όταν το
γίνεται μέγιστο όταν το  βρεθεί στην ίδια ευθεία με τα
βρεθεί στην ίδια ευθεία με τα  .
.Σας ευχαριστώ, Γιώργος.
Συντονιστές: vittasko, silouan, rek2
 και οι διάμεσοί του
και οι διάμεσοί του  που τέμνονται στο
που τέμνονται στο  . Το σημείο
. Το σημείο  διατρέχει την πλευρά
διατρέχει την πλευρά  .
.  και
και  με
με 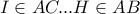 .
.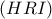 γίνεται μέγιστο όταν το
γίνεται μέγιστο όταν το  βρεθεί στην ίδια ευθεία με τα
βρεθεί στην ίδια ευθεία με τα  .
.Καλημέρα!Γιώργος Μήτσιος έγραψε: ↑Πέμ Ιαν 02, 2020 1:13 amΧαιρετώ. Αφετηρία για το παρόν είναι το θέμα τούτοΣυνευθειακά για μέγιστο.PNG
Δίνεται τρίγωνοκαι οι διάμεσοί του
που τέμνονται στο
. Το σημείο
διατρέχει την πλευρά
.
Φέρουμε τιςκαι
με
.
Να εξεταστεί αν τογίνεται μέγιστο όταν το
βρεθεί στην ίδια ευθεία με τα
.
Σας ευχαριστώ, Γιώργος.

 όμοια
όμοια 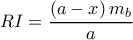
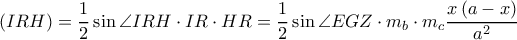
 σταθερό το
σταθερό το  μεγιστοποιείται όταν μεγιστοποιείται το
μεγιστοποιείται όταν μεγιστοποιείται το  δηλαδή όταν
δηλαδή όταν  (το οποίο συμβαίνει όταν
(το οποίο συμβαίνει όταν  συνευθειακά)
συνευθειακά) όπου
όπου  το σταθερό μέσο του
το σταθερό μέσο του  . (Το αφήνω
. (Το αφήνω  για ευκολία πληκτρολόγησης )
για ευκολία πληκτρολόγησης ) προς τις διαμέσους
προς τις διαμέσους  τέμνουν τις
τέμνουν τις  στα
στα  .
. διατρέχει το
διατρέχει το  ( αν διατρέχει το
( αν διατρέχει το 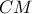 θα εργαστώ ομοίως)
θα εργαστώ ομοίως) προφανές ότι :
προφανές ότι : 
 , θα είναι :
, θα είναι : .
.  (αληθές)
(αληθές)  με το ίσον να ισχύει όταν
με το ίσον να ισχύει όταν  .
.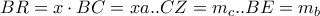 . Τότε
. Τότε  και
και  .
.  . Τότε
. Τότε  . Έχουμε
. Έχουμε  .
.  δηλ παραβολή
δηλ παραβολή  .Τότε η
.Τότε η  είναι διάμεσος και τα
είναι διάμεσος και τα 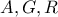 συνευθειακά.
συνευθειακά. η τομή των
η τομή των  . Τότε:
. Τότε: είναι ανεξάρτητο από τη θέση του δρομέα
είναι ανεξάρτητο από τη θέση του δρομέα  πάνω στην
πάνω στην  . Ευχαριστώ και πάλι, Γιώργος.
. Ευχαριστώ και πάλι, Γιώργος.Γιώργος Μήτσιος έγραψε: ↑Παρ Ιαν 03, 2020 6:24 pm
Σταθερό εμβαδόν.PNG
Έστωη τομή των
. Τότε:
Να δειχθεί ότι τοείναι ανεξάρτητο από τη θέση του δρομέα
πάνω στην
. Ευχαριστώ και πάλι, Γιώργος.
 να κινήται επί σταθερής ευθείας παράλληλης στην
να κινήται επί σταθερής ευθείας παράλληλης στην  (τότε το τρίγωνο θα έχει πάντοτε το ίδιο ύψος και ίδια βάση ,την
(τότε το τρίγωνο θα έχει πάντοτε το ίδιο ύψος και ίδια βάση ,την  ).
). η τομή
η τομή  με την
με την  αρκεί ο λόγος
αρκεί ο λόγος 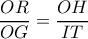 να είναι σταθερός.
να είναι σταθερός. ,τότε θα είναι
,τότε θα είναι 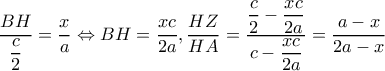
 και
και 
 διατέμνουσας
διατέμνουσας  είναι
είναι 


 τέμνει την
τέμνει την  στο
στο  . Το
. Το  είναι βαρύκεντρο οπότε παίρνουμε
είναι βαρύκεντρο οπότε παίρνουμε  (από τα όμοια τρίγωνα).
(από τα όμοια τρίγωνα).  . Έτσι
. Έτσι 

 είναι παραλληλόγραμμο με το
είναι παραλληλόγραμμο με το  κέντρο του άρα
κέντρο του άρα 
 κινείται στην μεσοπαράλληλη των
κινείται στην μεσοπαράλληλη των  και είναι
και είναι  ανεξάρτητο της θέσης του
ανεξάρτητο της θέσης του  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες