 και
και  τυχαία σημεία στο ημιεπίπεδο που ορίζει η
τυχαία σημεία στο ημιεπίπεδο που ορίζει η  και δεν ανήκει το
και δεν ανήκει το  .
.Θεωρούμε τις τομές:

Να δείξετε ότι οι
 τέμνονται πάνω στην
τέμνονται πάνω στην  .
.Συντονιστές: vittasko, silouan, rek2
 και
και  τυχαία σημεία στο ημιεπίπεδο που ορίζει η
τυχαία σημεία στο ημιεπίπεδο που ορίζει η  και δεν ανήκει το
και δεν ανήκει το  .
.
 τέμνονται πάνω στην
τέμνονται πάνω στην  .
.ΜεΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Δευ Σεπ 02, 2019 10:54 pm122.PNG
Έστω τρίγωνοκαι
τυχαία σημεία στο ημιεπίπεδο που ορίζει η
και δεν ανήκει το
.
Θεωρούμε τις τομές:
Να δείξετε ότι οιτέμνονται πάνω στην
.
 προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι προοπτικά οπότε σύμφωνα με το θεώρημα του Desargues τα σημεία τομής των αντιστοίχων πλευρών τους θα είναι συνευθειακά , δηλαδή τα
είναι προοπτικά οπότε σύμφωνα με το θεώρημα του Desargues τα σημεία τομής των αντιστοίχων πλευρών τους θα είναι συνευθειακά , δηλαδή τα  ,
,  ,
,  είναι συνευθειακά. Ομοίως από
είναι συνευθειακά. Ομοίως από  προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι προοπτικά οπότε σύμφωνα με το θεώρημα του Desargues τα σημεία τομής των αντιστοίχων πλευ
είναι προοπτικά οπότε σύμφωνα με το θεώρημα του Desargues τα σημεία τομής των αντιστοίχων πλευ ρών τους θα είναι συνευθειακά , δηλαδή το σημείο τομής των
ρών τους θα είναι συνευθειακά , δηλαδή το σημείο τομής των 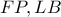 ανήκει στην ευθεία των σημείων τομής των δύο άλλων αντιστοίχων πλευρών τους, δηλαδή στην ευθεία
ανήκει στην ευθεία των σημείων τομής των δύο άλλων αντιστοίχων πλευρών τους, δηλαδή στην ευθεία 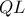 με
με  , δηλαδή
, δηλαδή  (αφού η
(αφού η  έτεμνε (από την πρώτη προοπτικότητα την ευθεία
έτεμνε (από την πρώτη προοπτικότητα την ευθεία  στο
στο  . Τότε όμως τα σημεία
. Τότε όμως τα σημεία  είναι συνευθειακά οπότε σύμφωνα με το αντίστροφο του Θεωρήματος Desargues τα τρίγωνα
είναι συνευθειακά οπότε σύμφωνα με το αντίστροφο του Θεωρήματος Desargues τα τρίγωνα  είναι προοπτικά και συνεπώς
είναι προοπτικά και συνεπώς 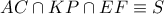 και το ζητούμενο έχει αποδειχθεί
και το ζητούμενο έχει αποδειχθεί . Θα δείξουμε ότι
. Θα δείξουμε ότι  συνευθειακά και όμοια θα είναι και
συνευθειακά και όμοια θα είναι και  συνευθειακά.
συνευθειακά. με διατέμνουσα
με διατέμνουσα 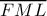 είναι:
είναι:
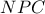 με διατέμνουσα
με διατέμνουσα  είναι:
είναι:
 με διατέμνουσα
με διατέμνουσα  είναι :
είναι :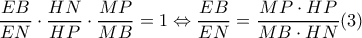
 παίρνουμε από το αντίστροφο του θεωρήματος Μενελάου στο
παίρνουμε από το αντίστροφο του θεωρήματος Μενελάου στο  ότι
ότι  συνευθειακά.
συνευθειακά.Μία ακόμη λύση για το πρόβλημα.ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Δευ Σεπ 02, 2019 10:54 pm122.PNG
Έστω τρίγωνοκαι
τυχαία σημεία στο ημιεπίπεδο που ορίζει η
και δεν ανήκει το
.
Θεωρούμε τις τομές:
Να δείξετε ότι οιτέμνονται πάνω στην
.
 το επίπεδο του τριγώνου του σχήματος και
το επίπεδο του τριγώνου του σχήματος και  ένα άλλο επίπεδο ώστε η
ένα άλλο επίπεδο ώστε η  να είναι ειδική ευθεία του επιπέδου
να είναι ειδική ευθεία του επιπέδου  για μία κεντρική προβολή κέντρου
για μία κεντρική προβολή κέντρου  .
. θα μετασχηματιστούν στο
θα μετασχηματιστούν στο  σε παράλληλες οπότε παίρνουμε το παρακάτω σχήμα στο οποίο
σε παράλληλες οπότε παίρνουμε το παρακάτω σχήμα στο οποίο  :
Πλέον τα πράγματα είναι αρκετά απλά αφού αρκεί να δείξουμε πως
:
Πλέον τα πράγματα είναι αρκετά απλά αφού αρκεί να δείξουμε πως  .
. και
και  οπότε
οπότε  ίσα και εύκολα
ίσα και εύκολα  ίσα άρα το
ίσα άρα το  είναι παραλληλόγραμμο .
είναι παραλληλόγραμμο .Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 2 επισκέπτες