 είναι το ύψος,
είναι το ύψος,  το ορθόκεντρο και
το ορθόκεντρο και  το περίκεντρο οξυγώνιου τριγώνου
το περίκεντρο οξυγώνιου τριγώνου  Ο περίκυκλος
Ο περίκυκλος του τριγώνου
 τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο 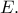 Να δείξετε ότι
Να δείξετε ότι 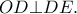
Συντονιστές: vittasko, silouan, rek2
 είναι το ύψος,
είναι το ύψος,  το ορθόκεντρο και
το ορθόκεντρο και  το περίκεντρο οξυγώνιου τριγώνου
το περίκεντρο οξυγώνιου τριγώνου  Ο περίκυκλος
Ο περίκυκλος  τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο 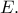 Να δείξετε ότι
Να δείξετε ότι 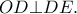
Καλησπέρα κ. Γιώργο και Καλό Πάσχα!george visvikis έγραψε: ↑Δευ Απρ 22, 2019 11:26 amείναι το ύψος,
το ορθόκεντρο και
το περίκεντρο οξυγώνιου τριγώνου
Ο περίκυκλος
του τριγώνουτέμνει την
στο
και η
την
στο
Να δείξετε ότι
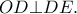
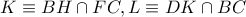 . Τότε, από το πλήρες τετράπλευρο
. Τότε, από το πλήρες τετράπλευρο 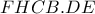 προκύπτει ότι τα
προκύπτει ότι τα 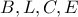 είναι αρμονικά συζυγή, και αφού
είναι αρμονικά συζυγή, και αφού 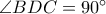 , έχουμε ότι
, έχουμε ότι 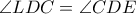 .
.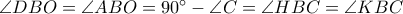 , και
, και 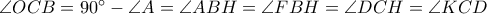 . Επομένως, τα
. Επομένως, τα  είναι ισογώνια συζυγή στο τρίγωνο
είναι ισογώνια συζυγή στο τρίγωνο  .
. 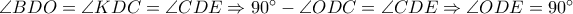 , και το ζητούμενο δείχτηκε.
, και το ζητούμενο δείχτηκε. το μέσο της πλευράς
το μέσο της πλευράς  . Τότε
. Τότε 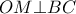 . Είναι γνωστό ότι, οι περιγεγραμμένοι κύκλοι
. Είναι γνωστό ότι, οι περιγεγραμμένοι κύκλοι  του
του  , και
, και  του τριγώνου
του τριγώνου  , είναι συμμετρικοί ως προς την πλευρά
, είναι συμμετρικοί ως προς την πλευρά  . Έστω
. Έστω 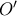 το κέντρο του
το κέντρο του  , και
, και 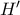 το συμμετρικό του
το συμμετρικό του  ως προς τη
ως προς τη  . Τότε
. Τότε 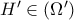 .
. το μέσο του
το μέσο του  . Τότε
. Τότε 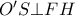 (
(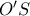 απόστημα της χορδής
απόστημα της χορδής  του κύκλου
του κύκλου  .) Ως εκ τούτου, αν
.) Ως εκ τούτου, αν  το συμμετρικό του
το συμμετρικό του  ως προς τη
ως προς τη  , τότε
, τότε 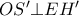 (Ο μετασχηματισμός της συμμετρίας ως προς ευθεία, διατηρεί την γωνία δύο ευθειών).
(Ο μετασχηματισμός της συμμετρίας ως προς ευθεία, διατηρεί την γωνία δύο ευθειών). , προκύπτει ότι τα σηµεία
, προκύπτει ότι τα σηµεία  ,
,  ,
,  και
και  ανήκουν στον ίδιο κύκλο, και εφόσον
ανήκουν στον ίδιο κύκλο, και εφόσον 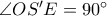 , τότε και
, τότε και 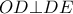 .
. Δίνεται τρίγωνο
Δίνεται τρίγωνο  και ένα σηµείο
και ένα σηµείο  . Φέρουµε τις κάθετες
. Φέρουµε τις κάθετες  ,
,  και
και  στις
στις  ,
,  και
και  ', στα σηµεία
', στα σηµεία  ,
,  και
και  , αντίστοιχα. Οι ευθείες
, αντίστοιχα. Οι ευθείες  ,
,  και
και  διέρχονται από το ίδιο σηµείο, όταν και µόνον όταν, τα σηµεία
διέρχονται από το ίδιο σηµείο, όταν και µόνον όταν, τα σηµεία  ,
,  ,
,  και
και  είναι οµοκυκλικά.
είναι οµοκυκλικά. το μέσο της πλευράς
το μέσο της πλευράς  . Τότε
. Τότε 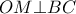 . Είναι γνωστό ότι, οι περιγεγραμμένοι κύκλοι
. Είναι γνωστό ότι, οι περιγεγραμμένοι κύκλοι  του
του  , και
, και  του τριγώνου
του τριγώνου  , είναι συμμετρικοί ως προς την πλευρά
, είναι συμμετρικοί ως προς την πλευρά  . Έστω
. Έστω 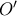 το κέντρο του
το κέντρο του  , και
, και 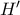 το συμμετρικό του
το συμμετρικό του  ως προς τη
ως προς τη  . Τότε
. Τότε 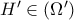 .
. το μέσο του
το μέσο του  . Τότε
. Τότε 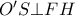 (
(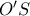 απόστημα της χορδής
απόστημα της χορδής  του κύκλου
του κύκλου  .) Ως εκ τούτου, αν
.) Ως εκ τούτου, αν  το συμμετρικό του
το συμμετρικό του  ως προς τη
ως προς τη  , τότε
, τότε 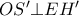 (Ο μετασχηματισμός της συμμετρίας ως προς ευθεία, διατηρεί την γωνία δύο ευθειών).
(Ο μετασχηματισμός της συμμετρίας ως προς ευθεία, διατηρεί την γωνία δύο ευθειών). και
και  ανήκουν σε κύκλο διαμέτρου
ανήκουν σε κύκλο διαμέτρου  . Αρκεί να αποδείξουμε ότι και το
. Αρκεί να αποδείξουμε ότι και το  ανήκει σε αυτόν τον κύκλο.
ανήκει σε αυτόν τον κύκλο. στον κύκλο
στον κύκλο  προκύπτει ότι
προκύπτει ότι 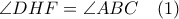 .
. το μέσο του
το μέσο του  , τότε από στο ορθογώνιο τρίγωνο
, τότε από στο ορθογώνιο τρίγωνο  , η
, η  διάμεσος επί την υποτείνουσα, οπότε
διάμεσος επί την υποτείνουσα, οπότε  ,
,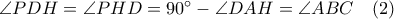 .
. και
και  προκύπτει ότι
προκύπτει ότι 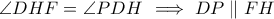 . Επομένως, το
. Επομένως, το  είναι παραλληλόγραμμο, και εφόσον
είναι παραλληλόγραμμο, και εφόσον 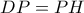 είναι ρόμβος, δηλαδή,
είναι ρόμβος, δηλαδή, 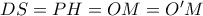 , και εφόσον
, και εφόσον 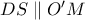 , τότε το
, τότε το  παραλληλόγραμμο, οπότε
παραλληλόγραμμο, οπότε 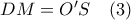 .
. είναι ισοσκελές τραπέζιο, επειδή
είναι ισοσκελές τραπέζιο, επειδή 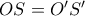 (συμμετρικά ως προς τη
(συμμετρικά ως προς τη  ). Επομένως,
). Επομένως, 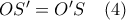 .
. και
και  έχουμε ότι,
έχουμε ότι, 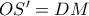 , οπότε και το τραπέζιο
, οπότε και το τραπέζιο 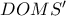 είναι ισοσκελές, και επομένως εγγράψιμο, δηλαδή, το
είναι ισοσκελές, και επομένως εγγράψιμο, δηλαδή, το  ανήκει στον ίδιο κύκλο με τα σημεία
ανήκει στον ίδιο κύκλο με τα σημεία  ,
,  και
και  , που είναι αυτό που θέλαμε να αποδείξουμε.
, που είναι αυτό που θέλαμε να αποδείξουμε.george visvikis έγραψε: ↑Δευ Απρ 22, 2019 11:26 amΆλλη μία όμορφη καθετότητα.png
είναι το ύψος,
το ορθόκεντρο και
το περίκεντρο οξυγώνιου τριγώνου
Ο περίκυκλος
του τριγώνουτέμνει την
στο
και η
την
στο
Να δείξετε ότι
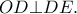
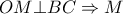 μέσον της
μέσον της  και
και  είναι διάμεσος προς την υποτείνουσα στο
είναι διάμεσος προς την υποτείνουσα στο 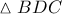
 όπως και των
όπως και των  με
με 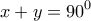
 ορθόκεντρο του
ορθόκεντρο του 
 μέσον της
μέσον της  και
και  παραλ/μμο.Άρα
παραλ/μμο.Άρα 
 Το τρίγωνο
Το τρίγωνο  είναι ισοσκελές με
είναι ισοσκελές με  , από
, από  και άρα, το σημείο
και άρα, το σημείο  ταυτίζεται με το μέσον του τμήματος
ταυτίζεται με το μέσον του τμήματος 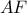 , λόγω
, λόγω 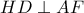 .
. το μέσον του
το μέσον του  και έχουμε
και έχουμε 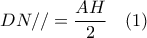
 και
και 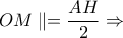
 όπου
όπου  είναι το περίκεντρο του
είναι το περίκεντρο του  και
και  είναι το μέσον της πλευράς
είναι το μέσον της πλευράς  .
. του τριγώνου
του τριγώνου  είναι συμμετρικός του περίκυκλου
είναι συμμετρικός του περίκυκλου  του
του  και άρα, έχουμε
και άρα, έχουμε 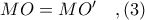 όπου
όπου 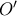 είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  .
.
 Από το πλήρες τετράπλευρο
Από το πλήρες τετράπλευρο 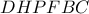 , όπου
, όπου  , έχουμε ότι η ευθεία
, έχουμε ότι η ευθεία  περνάει από το μέσον
περνάει από το μέσον  του
του 
 Ευθεία Gauss-Newton
Ευθεία Gauss-Newton  .
. και
και  τώρα, προκύπτει ότι
τώρα, προκύπτει ότι 
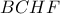 έχουμε ότι η ευθεία
έχουμε ότι η ευθεία  ταυτίζεται με την Πολική ευθεία του σημείου
ταυτίζεται με την Πολική ευθεία του σημείου  ως προς τον κύκλο
ως προς τον κύκλο 
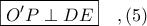
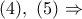
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.Ας δούμε και μια διαφορετική προσέγγιση του όμορφου προβλήματος συμμετέχοντας στην γεωμετρική παρέα των "ΜΕΓΑΛΩΝ" !!!!!george visvikis έγραψε: ↑Δευ Απρ 22, 2019 11:26 amΆλλη μία όμορφη καθετότητα.png
είναι το ύψος,
το ορθόκεντρο και
το περίκεντρο οξυγώνιου τριγώνου
Ο περίκυκλος
του τριγώνουτέμνει την
στο
και η
την
στο
Να δείξετε ότι
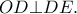
 προκύπτει ότι
προκύπτει ότι 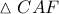 ισοσκελές και με
ισοσκελές και με 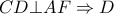 το μέσο της . Αν
το μέσο της . Αν  οι ορθές προβολές των
οι ορθές προβολές των  επί της
επί της  ( προφανώς
( προφανώς  το μέσο της
το μέσο της  (κέντρο του περίκυκλου του ορθογωνίου στο
(κέντρο του περίκυκλου του ορθογωνίου στο  τριγώνου
τριγώνου  )) και
)) και  οι ορθές προβολές των
οι ορθές προβολές των 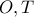 επί της
επί της  , τότε με
, τότε με  τα μέσα των
τα μέσα των 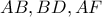 αντίστοιχα προκύπτει ότι:
αντίστοιχα προκύπτει ότι: 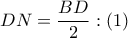 και
και 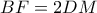 . Από (γενικευμένο Nagel ) προκύπτει ότι
. Από (γενικευμένο Nagel ) προκύπτει ότι  οπότε σύμφωνα με το Stathis koutras Theorem προκύπτει ότι:
οπότε σύμφωνα με το Stathis koutras Theorem προκύπτει ότι: 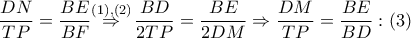
 σύμφωνα με το αντίστροφο του περιώνυμου Θεωρήματος προκύπτει ότι
σύμφωνα με το αντίστροφο του περιώνυμου Θεωρήματος προκύπτει ότι 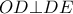 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. το σημείο τομής της
το σημείο τομής της  με τον περιγεγραμμένο κύκλο του
με τον περιγεγραμμένο κύκλο του  .
.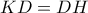 και
και  , άρα
, άρα 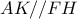 .
.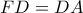 .
. τέμνει την
τέμνει την  στο
στο  .
. .
. προκύπτει τώρα εύκολα ότι
προκύπτει τώρα εύκολα ότι 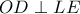 .
.Διονύσιος Αδαμόπουλος έγραψε: ↑Τετ Απρ 24, 2019 7:21 pmΔιαφορετικά:
Έστωτο σημείο τομής της
με τον περιγεγραμμένο κύκλο του
.
Προφανώς είναικαι
, άρα
.
Έπεται λοιπόν από Θαλή πως.
Έστω πως ητέμνει την
στο
.
Τότε πάλι από Θαλή είναι.
Από Θεώρημα πεταλούδας στο εγγράψιμοπροκύπτει τώρα εύκολα ότι
.
Το σχήμα στην πολύ ωραία λύση του ΔιονύσηΔιονύσιος Αδαμόπουλος έγραψε: ↑Τετ Απρ 24, 2019 7:21 pmΔιαφορετικά:
Έστωτο σημείο τομής της
με τον περιγεγραμμένο κύκλο του
.
Προφανώς είναικαι
, άρα
.
Έπεται λοιπόν από Θαλή πως.
Έστω πως ητέμνει την
στο
.
Τότε πάλι από Θαλή είναι.
Από Θεώρημα πεταλούδας στο εγγράψιμοπροκύπτει τώρα εύκολα ότι
.
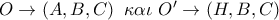 είναι ίσοι και άρα στην ιδία γωνία
είναι ίσοι και άρα στην ιδία γωνία  αντιστοιχούν ίσες χορδές , οπότε
αντιστοιχούν ίσες χορδές , οπότε  .
. του ορθοκέντου
του ορθοκέντου  ανήκει στον κύκλο
ανήκει στον κύκλο  το τετράπλευρο
το τετράπλευρο  είναι ρόμβος οπότε τα τρίγωνα
είναι ρόμβος οπότε τα τρίγωνα 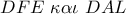 είναι ίσα .
είναι ίσα .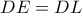 και από το Θ. Πεταλούδας
και από το Θ. Πεταλούδας 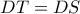 και άρα η
και άρα η 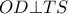
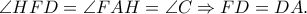 Έστω
Έστω 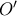 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Τότε
. Τότε 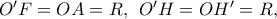 όπου
όπου  η ακτίνα του κύκλου
η ακτίνα του κύκλου  Επομένως οι κύκλοι
Επομένως οι κύκλοι 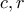 είναι ίσοι και οι
είναι ίσοι και οι  έχουν κοινή χορδή την
έχουν κοινή χορδή την  .
.  είναι ριζικό κέντρο των τριών αυτών κύκλων, έχουμε άμεσα την απόδειξη.
είναι ριζικό κέντρο των τριών αυτών κύκλων, έχουμε άμεσα την απόδειξη. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 21 επισκέπτες