 και
και  σημείο της
σημείο της  .
.Ο κύκλος που διέρχεται από το
 και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει τις
τέμνει τις  στα
στα  αντίστοιχα.
αντίστοιχα.Αν η
 συναντά τον περίκυκλο του
συναντά τον περίκυκλο του  στο
στο  , δείξτε ότι:
, δείξτε ότι:a.

b.

c.
![[AEQD]=3[QBC] [AEQD]=3[QBC]](/forum/ext/geomar/texintegr/latexrender/pictures/ce27ba2038ba2325c81db0357ee15aec.png)
Συντονιστές: vittasko, silouan, rek2
 και
και  σημείο της
σημείο της  .
. και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει τις
τέμνει τις  στα
στα  αντίστοιχα.
αντίστοιχα. συναντά τον περίκυκλο του
συναντά τον περίκυκλο του  στο
στο  , δείξτε ότι:
, δείξτε ότι:

![[AEQD]=3[QBC] [AEQD]=3[QBC]](/forum/ext/geomar/texintegr/latexrender/pictures/ce27ba2038ba2325c81db0357ee15aec.png)
 η πλευρά του ισοπλεύρου.
Από τα εγγεγραμμένα τετράπλευρα
η πλευρά του ισοπλεύρου.
Από τα εγγεγραμμένα τετράπλευρα  και τις σχέσεις εγγεγραμμένων γωνιών και γωνιών χορδής
και τις σχέσεις εγγεγραμμένων γωνιών και γωνιών χορδής  και των
και των  έχουμε:
έχουμε:

 είναι όμοια:
είναι όμοια: 

Για να μην μείνει αναπάντητο το iii) πανέμορφο ερώτημα του Θάνου (ΑΡΙΣΤΟΥ ΣΥΝΘΕΤΗ ΓΕΩΜΕΤΡΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ ΠΑΓΚΟΣΜΙΩΣ ΔΙΑΚΕΚΡΙΜΕΝΟΥ !)
 Έστω
Έστω  και
και 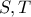 είναι οι ορθές προβολές των
είναι οι ορθές προβολές των 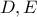 και
και  επί της
επί της  και
και  αντίστοιχα. Προφανώς
αντίστοιχα. Προφανώς 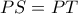 αφού
αφού  διχοτόμος (από τις
διχοτόμος (από τις  άρες) της
άρες) της  . Τότε
. Τότε 


 Από την προφανή ομοιότητα των ορθογωνίων τριγώνων
Από την προφανή ομοιότητα των ορθογωνίων τριγώνων  και ομοίως
και ομοίως 

 Ισχύει:
Ισχύει: 
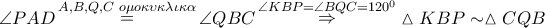
 άρα και
άρα και 
 Από
Από  και ομοίως
και ομοίως  οπότε
οπότε 
 , όπου
, όπου  είναι το μήκος της πλευράς του ισοπλεύρου
είναι το μήκος της πλευράς του ισοπλεύρου 

 και με όμοιο τρόπο προκύπτει ότι:
και με όμοιο τρόπο προκύπτει ότι:  .
. Από
Από 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης