ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Σάβ Ιουν 23, 2018 12:24 pm
Η αρχική λύση που έκανα ήταν με Αναλυτική Γεωμετρία.
Θα γράψω μια λύση με Μιγαδικούς
(Ιδιες είναι απλώς με Μιγαδικούς έχει λιγότερο γράψιμο)
Θεωρούμε ότι τα κοινά σημεία των κύκλων είναι τα

Ετσι τα κέντρα τους θα είναι στον πραγματικό άξονα και η εξίσωση
ενός από αυτούς θα είναι

Οι δύο ευθείες θα έχουν εξισώσεις

και

Οπου

(Να σημειώσω ότι

)
Η πρώτη ευθεία τέμνει τον κύκλο όταν

στό

ενώ η δεύτερη για

στο

Μέσο του

είναι το

όπου

παράσταση που εξαρτάται μόνο από τα

Αν θέσουμε

τότε εύκολα βλέπουμε ότι το μέσο βρίσκεται πάνω στην ευθεία
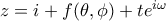
Η ίδια απόδειξη δουλεύει αν δεν πάρουμε το μέσο αλλά ένα σημείο που χωρίζει σε σταθερό λόγο.
Ωραία λύση, αλλά όταν είπατε απλή λύση, περίμενα καμιά απλή μετρική ή κατασκευαστική, όχι μιγαδικούς (αιρετικά εργαλεία

) .
Η δικιά μου λύση:
Καταρχάς θα χρησιμοποιήσουμε την εξής ιδιότητα-λήμμα:
Έστω συνευθειακά σημεία

και φέρνουμε από τα

παράλληλες ευθείες. Σε κάθε μια από αυτές παίρνουμε τα σημεία

αντίστοιχα.
Αν

, τότε για να είναι και τα

συνευθειακά πρέπει

και αντίστροφα.
Απόδειξη:
Φέρνουμε από τα

και

κάθετες ευθείες στις τρεις παράλληλες. Έστω πως τέμνουν λοιπόν την

στα

αντίστοιχα και την
στα

αντίστοιχα.
Ισχύει προφανώς από όμοια τρίγωνα πως

.
Για να είναι τα

συνευθειακά πρέπει

και αντίστροφα.
Όμως προφανώς

, άρα πρέπει

Ισχύει ότι

, άρα πρέπει
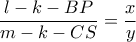
.
Όμως

, άρα καταλήγουμε στο ότι πρέπει

για να είναι τα

συνευθειακά και αντίστροφα.

- Λήμμα Σ1.png (14.46 KiB) Προβλήθηκε 731 φορές
Πίσω στην άσκηση:
Θα αποδείξουμε την άσκηση για τρεις κύκλους και επαγωγικά αποδεικνύεται και για

.
Φέρνουμε από το

μια ευθεία

η οποία τέμνει τους

κύκλους στα σημεία

και

.
Παρατηρούμε πως οι

και

είναι παράλληλες. Αυτό ισχύει επειδή

, από τα εγγράψιμα

και

.
Άρα γενικότερα οι

,

και
είναι παράλληλες.
Για ακριβώς τον ίδιο λόγο παράλληλες είναι και

,

και

.
Θεωρούμε

τα μέσα των

,

και
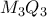
αντίστοιχα. Αυτά είναι συνευθειακά, καθώς η ευθειά που διέρχεται από οποιαδήποτε δύο από αυτά περνάει από σταθερό σημείο, το σημείο τομής των

και

(αυτό βασίζεται σε γνωστό λήμμα).
Παρατηρούμε ακόμα πως η

είναι παράλληλη στην

, η

είναι παράλληλη στην

και η

είναι παράλληλη στην

και λόγω της παραλληλίας των

,

και

, προκύπτει πως και οι

είναι παράλληλες. Αρκεί να εφαρμόσουμε τώρα τον ισχυρισμό που αποδείξαμε παραπάνω.
Αρκεί δηλαδή να αποδειχθεί πως
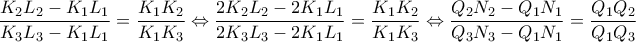
(το δεύτερο μέρος προέκυψε από Θεώρημα Θαλή), το οποίο ισχύει, από το αντίστροφο του λήμματος για τις συνευθειακές τριάδες

και

.

- Λήμμα Σ2.png (39.61 KiB) Προβλήθηκε 731 φορές
 δύο σημεία και
δύο σημεία και  κύκλοι, με την ιδιότητα να διέρχονται όλοι τους από τα σημεία
κύκλοι, με την ιδιότητα να διέρχονται όλοι τους από τα σημεία  .
. δύο ευθείες
δύο ευθείες  και
και  . Η
. Η  τέμνει τους κύκλους
τέμνει τους κύκλους  στα σημεία
στα σημεία  αντίστοιχα, ενώ η
αντίστοιχα, ενώ η  στα
στα  αντίστοιχα. Έστω
αντίστοιχα. Έστω  τα μέσα των
τα μέσα των  αντίστοιχα. Να αποδειχθεί ότι τα
αντίστοιχα. Να αποδειχθεί ότι τα  είναι συνευθειακά!
είναι συνευθειακά!





 )
) στό
στό 
 στο
στο 
 είναι το
είναι το 
 παράσταση που εξαρτάται μόνο από τα
παράσταση που εξαρτάται μόνο από τα 

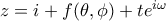
 και φέρνουμε από τα
και φέρνουμε από τα  αντίστοιχα.
αντίστοιχα. , τότε για να είναι και τα
, τότε για να είναι και τα  και αντίστροφα.
και αντίστροφα. κάθετες ευθείες στις τρεις παράλληλες. Έστω πως τέμνουν λοιπόν την
κάθετες ευθείες στις τρεις παράλληλες. Έστω πως τέμνουν λοιπόν την  στα
στα  αντίστοιχα και την
αντίστοιχα και την  στα
στα  αντίστοιχα.
αντίστοιχα. .
. και αντίστροφα.
και αντίστροφα. , άρα πρέπει
, άρα πρέπει 
 , άρα πρέπει
, άρα πρέπει 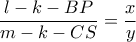 .
.  .
. μια ευθεία
μια ευθεία  η οποία τέμνει τους
η οποία τέμνει τους  κύκλους στα σημεία
κύκλους στα σημεία  και
και  .
. και
και  είναι παράλληλες. Αυτό ισχύει επειδή
είναι παράλληλες. Αυτό ισχύει επειδή  , από τα εγγράψιμα
, από τα εγγράψιμα  και
και  .
. είναι παράλληλες.
είναι παράλληλες. ,
,  και
και  .
. τα μέσα των
τα μέσα των  είναι παράλληλη στην
είναι παράλληλη στην  είναι παράλληλη στην
είναι παράλληλη στην  είναι παράλληλες. Αρκεί να εφαρμόσουμε τώρα τον ισχυρισμό που αποδείξαμε παραπάνω.
είναι παράλληλες. Αρκεί να εφαρμόσουμε τώρα τον ισχυρισμό που αποδείξαμε παραπάνω.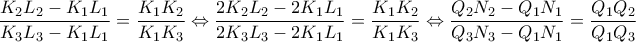 (το δεύτερο μέρος προέκυψε από Θεώρημα Θαλή), το οποίο ισχύει, από το αντίστροφο του λήμματος για τις συνευθειακές τριάδες
(το δεύτερο μέρος προέκυψε από Θεώρημα Θαλή), το οποίο ισχύει, από το αντίστροφο του λήμματος για τις συνευθειακές τριάδες  και
και  .
.