 με περιγεγραμμένο κύκλο
με περιγεγραμμένο κύκλο 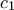 και έστω ότι ο εγγεγραμμένος κύκλος του εφάπτεται στις
και έστω ότι ο εγγεγραμμένος κύκλος του εφάπτεται στις  στα
στα  . Έστω
. Έστω  το μέσο του τόξου
το μέσο του τόξου  . Ακόμα έστω
. Ακόμα έστω  σημείο του τμήματος
σημείο του τμήματος  ώστε
ώστε  . Η
. Η  τέμνει τον
τέμνει τον 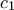 στο
στο  . Να αποδειχθεί ότι η
. Να αποδειχθεί ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία  .
.Συντονιστές: vittasko, silouan, rek2
 με περιγεγραμμένο κύκλο
με περιγεγραμμένο κύκλο 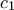 και έστω ότι ο εγγεγραμμένος κύκλος του εφάπτεται στις
και έστω ότι ο εγγεγραμμένος κύκλος του εφάπτεται στις  στα
στα  . Έστω
. Έστω  το μέσο του τόξου
το μέσο του τόξου  . Ακόμα έστω
. Ακόμα έστω  σημείο του τμήματος
σημείο του τμήματος  ώστε
ώστε  . Η
. Η  τέμνει τον
τέμνει τον 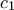 στο
στο  . Να αποδειχθεί ότι η
. Να αποδειχθεί ότι η  διχοτομεί τη γωνία
διχοτομεί τη γωνία  .
. το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  και
και  το άλλο σημείο τομής του
το άλλο σημείο τομής του  του τριγώνου
του τριγώνου  με τον κύκλο
με τον κύκλο 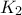 , διαμέτρου
, διαμέτρου  .
. 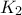 με πόλο το σημείο του
με πόλο το σημείο του  και δύναμη αντιστροφής
και δύναμη αντιστροφής 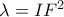 είναι η ευθεία
είναι η ευθεία  .
.  .)
.)  έχει αντίστροφο το σημείο τομής, έστω
έχει αντίστροφο το σημείο τομής, έστω  , της
, της  με τη
με τη  . Το
. Το  είναι προφανώς μέσο του
είναι προφανώς μέσο του  .
.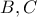 αντιστοιχίζονται στο μέσα των
αντιστοιχίζονται στο μέσα των  .
. στο τρίγωνο
στο τρίγωνο  . Έτσι το
. Έτσι το  αντιστοιχίζεται στο
αντιστοιχίζεται στο  , πόδα του ύψους και η
, πόδα του ύψους και η  διέρχεται έτσι από το
διέρχεται έτσι από το  .
. το αντιδιαμετρικό του
το αντιδιαμετρικό του  ( στον κύκλο
( στον κύκλο  ).
).  ως προς τον εγγεγραμμένο κύκλο
ως προς τον εγγεγραμμένο κύκλο  είναι η ευθεία
είναι η ευθεία  που τέμνει την
που τέμνει την  έστω στο
έστω στο  .
.  θα διέρχεται από το
θα διέρχεται από το  . Το τετράπλευρο
. Το τετράπλευρο  είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  που έχει φορέα την ευθεία
που έχει φορέα την ευθεία  .
. θα διέρχεται έτσι από το
θα διέρχεται έτσι από το  είναι δηλαδή η
είναι δηλαδή η  και συνεπώς τα σημεία
και συνεπώς τα σημεία  είναι αρμονικά συζυγή των
είναι αρμονικά συζυγή των 
 , αυτή (η
, αυτή (η 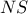 ) θα διχοτομεί τη γωνία
) θα διχοτομεί τη γωνία  .
. η τομή της
η τομή της  με την
με την  . Είναι γνωστό πως η τετράδα
. Είναι γνωστό πως η τετράδα 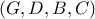 είναι αρμονική (αφού οι
είναι αρμονική (αφού οι  συντρέχουν στο
συντρέχουν στο  και θα σχηματιστεί το πλήρες τετράπλευρο
και θα σχηματιστεί το πλήρες τετράπλευρο  κλπ).
κλπ).  , προκύπτει από γνωστή ιδιότητα πως η
, προκύπτει από γνωστή ιδιότητα πως η 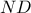 είναι διχοτόμος της
είναι διχοτόμος της  . Αφού είναι
. Αφού είναι  , προκύπτει ότι
, προκύπτει ότι 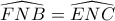 (1)
(1) , άρα αφού
, άρα αφού  είναι το μέσο του τόξου
είναι το μέσο του τόξου  , έχουμε πως
, έχουμε πως  .
. .
.  , προκύπτει ότι το
, προκύπτει ότι το  είναι εγγράψιμο τετράπλευρο. Όμοια και το
είναι εγγράψιμο τετράπλευρο. Όμοια και το 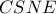 είναι εγγράψιμο τετράπλευρο.
είναι εγγράψιμο τετράπλευρο. και
και  . Από την (1) λοιπόν προκύπτει ότι
. Από την (1) λοιπόν προκύπτει ότι 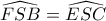 .
. διχοτομεί την
διχοτομεί την  , προκύπτει ότι η
, προκύπτει ότι η  διχοτομεί την
διχοτομεί την  .
. είναι εγγράψιμα αφού
είναι εγγράψιμα αφού 
 Όμως είναι
Όμως είναι 
 προκύπτει ότι
προκύπτει ότι 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες