 το μέσο του τόξου
το μέσο του τόξου  του περίκυκλου
του περίκυκλου  τριγώνου
τριγώνου  στο οποίο δεν ανήκει το
στο οποίο δεν ανήκει το  και
και  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του τριγώνου
του τριγώνου  με τις
με τις  αντίστοιχα. Να δειχθεί ότι
αντίστοιχα. Να δειχθεί ότι  , με
, με  όπου
όπου  ,
,
Στάθης
Συντονιστές: vittasko, silouan, rek2
 το μέσο του τόξου
το μέσο του τόξου  του περίκυκλου
του περίκυκλου  τριγώνου
τριγώνου  στο οποίο δεν ανήκει το
στο οποίο δεν ανήκει το  και
και  τα σημεία επαφής του έγκυκλου
τα σημεία επαφής του έγκυκλου  του τριγώνου
του τριγώνου  με τις
με τις  αντίστοιχα. Να δειχθεί ότι
αντίστοιχα. Να δειχθεί ότι  , με
, με  όπου
όπου  ,
,
Καλημέρα Στάθη! Πολύ ωραία άσκηση! ΕίναιΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε:παραλληλία από επαφές και τομές.pngΈστωτο μέσο του τόξου
του περίκυκλου
τριγώνου
στο οποίο δεν ανήκει το
και
τα σημεία επαφής του έγκυκλου
του τριγώνου
με τις
αντίστοιχα. Να δειχθεί ότι
, με
όπου
,
Στάθης
 . Αρκεί να δείξω ότι
. Αρκεί να δείξω ότι  . Από θεώρημα διχοτόμου στο
. Από θεώρημα διχοτόμου στο  :
: κι επειδή οι κόκκινες γωνίες είναι ίσες (εγγεγραμμένες στο ίδιο τόξο), τα τρίγωνα
κι επειδή οι κόκκινες γωνίες είναι ίσες (εγγεγραμμένες στο ίδιο τόξο), τα τρίγωνα 
 , άρα το
, άρα το  είναι εγγράψιμο,
είναι εγγράψιμο,  και
και  είναι το μέσο του τόξου
είναι το μέσο του τόξου  , οπότε η
, οπότε η 
 .
. , άρα τα τρίγωνα
, άρα τα τρίγωνα  είναι όμοια, οπότε
είναι όμοια, οπότε  , δηλαδή η
, δηλαδή η  είναι διχοτόμος
είναι διχοτόμος κι επειδή
κι επειδή  , θα είναι
, θα είναι 
Γιώργοgeorge visvikis έγραψε:Καλημέρα Στάθη! Πολύ ωραία άσκηση!ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε:παραλληλία από επαφές και τομές.pngΈστωτο μέσο του τόξου
του περίκυκλου
τριγώνου
στο οποίο δεν ανήκει το
και
τα σημεία επαφής του έγκυκλου
του τριγώνου
με τις
αντίστοιχα. Να δειχθεί ότι
, με
όπου
,
Στάθης
Παράλληλες από επαφές και τομές.png
Είναι. Αρκεί να δείξω ότι
. Από θεώρημα διχοτόμου στο
:
κι επειδή οι κόκκινες γωνίες είναι ίσες (εγγεγραμμένες στο ίδιο τόξο), τα τρίγωνα

θα είναι όμοια., άρα το
είναι εγγράψιμο,
και
είναι το μέσο του τόξου
, οπότε η

είναι διχοτόμος της γωνίας.
, άρα τα τρίγωνα
είναι όμοια, οπότε
, δηλαδή η
είναι διχοτόμος
της γωνίαςκι επειδή
, θα είναι
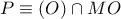 και
και  .
. Σύμφωνα με το παρακάτω Λήμμα 1 , έχουμε
Σύμφωνα με το παρακάτω Λήμμα 1 , έχουμε  και άρα, ισχύει
και άρα, ισχύει  λόγω του εγγραψίμου τετραπλεύρου
λόγω του εγγραψίμου τετραπλεύρου  , από
, από  .
. κάθετη ευθεία επί την
κάθετη ευθεία επί την  , τέμνει την ευθεία
, τέμνει την ευθεία  στο σημείο έστω
στο σημείο έστω  .
. , η προβολή του
, η προβολή του  επί της
επί της  και αρκεί ως ισοδύναμο ζητούμενο να αποδειχθεί ότι
και αρκεί ως ισοδύναμο ζητούμενο να αποδειχθεί ότι  , όπου
, όπου  .
.
 Σύμφωνα με το παρακάτω Λήμμα 2 , έχουμε
Σύμφωνα με το παρακάτω Λήμμα 2 , έχουμε  όπου
όπου  , είναι το σημείο τομής της ευθείας
, είναι το σημείο τομής της ευθείας  , από την δια του σημείου
, από την δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  .
. , λόγω
, λόγω  , έχουμε
, έχουμε 
 και
και  ( γνωστό αποτέλεσμα ), προκύπτει
( γνωστό αποτέλεσμα ), προκύπτει 

 και
και  , λόγω
, λόγω 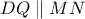 , προκύπτει
, προκύπτει  και άρα, τα σημεία
και άρα, τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. και το ισοδύναμο ζητούμενο έχει αποδιεχθεί.
και το ισοδύναμο ζητούμενο έχει αποδιεχθεί. εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  και έστω
και έστω  , τα σημεία επαφής του έγκυκλου
, τα σημεία επαφής του έγκυκλου  , στις πλευρές του
, στις πλευρές του  , αντιστοίχως. Αποδείξτε ότι
, αντιστοίχως. Αποδείξτε ότι  , όπου
, όπου  και
και  το έγκεντρο του
το έγκεντρο του  και
και  , το μέσον του τόξου
, το μέσον του τόξου  ππου δεν περιέχει του σημείο
ππου δεν περιέχει του σημείο  .
. εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  και έστω
και έστω  , τα σημεία επαφής του έγκυκλου
, τα σημεία επαφής του έγκυκλου  , στις πλευρές του
, στις πλευρές του  , αντιστοίχως. Αποδείξτε ότι
, αντιστοίχως. Αποδείξτε ότι  , όπου
, όπου  είναι το ύψος του
είναι το ύψος του  και
και  , το σημείο τομής της ευθείας
, το σημείο τομής της ευθείας  από την δια του σημείου
από την δια του σημείου  κάθετη ευθεία επί την
κάθετη ευθεία επί την  .
.Μία γρήγορη απόδειξη γι' αυτό είναι η παρακάτω.vittasko έγραψε: ΛΗΜΜΑ 1. - Δίνεται τρίγωνοεγγεγραμμένο σε κύκλο
και έστω
, τα σημεία επαφής του έγκυκλου
, στις πλευρές του
, αντιστοίχως. Αποδείξτε ότι
, όπου
και
το έγκεντρο του
και
, το μέσον του τόξου
ππου δεν περιέχει του σημείο
.
 και ακτίνας
και ακτίνας  . Τότε ο
. Τότε ο  γίνεται η ευθεία
γίνεται η ευθεία  . Επομένως το
. Επομένως το  πηγαίνει στο ίχνος της διχοτόμου, έστω
πηγαίνει στο ίχνος της διχοτόμου, έστω  και το
και το  πηγαίνει στο
πηγαίνει στο  . Επομένως
. Επομένως  .
.
 έπεται ότι
έπεται ότι 
 και άρα
και άρα  ομοκυκλικές τετράδες με τρία κοινά σημεία, οπότε τα σημεία
ομοκυκλικές τετράδες με τρία κοινά σημεία, οπότε τα σημεία  ανήκουν στον ίδιο κύκλο.
ανήκουν στον ίδιο κύκλο.



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες