Βρείτε όλες τις μονότονες συναρτήσεις
 τέτοιες ώστε
τέτοιες ώστε
να ισχύει για κάθε χ,y

Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε

Γράφουμε



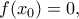 για κάποιο
για κάποιο 

 τώρα παίρνουμε λογάριθμο και στα δύο μέλη που δίνει
τώρα παίρνουμε λογάριθμο και στα δύο μέλη που δίνει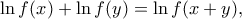
 ικανοποιεί Cauchy, και επειδή είναι μονότονη έχουμε διαδοχικά
ικανοποιεί Cauchy, και επειδή είναι μονότονη έχουμε διαδοχικά  , για κάποια σταθερά
, για κάποια σταθερά  (Λόγω πυκνότητας του
(Λόγω πυκνότητας του  στο
στο  .)
.)
Μια μικρή παρατήρηση ...θα είναιthepigod762 έγραψε: ↑Δευ Νοέμ 07, 2022 10:33 pmΓράφουμε
όπου
Σαφώς,
και γιαγια κάποιο
που ικανοποιεί.
Γιατώρα παίρνουμε λογάριθμο και στα δύο μέλη που δίνει
οπότε ηικανοποιεί Cauchy, και επειδή είναι μονότονη έχουμε διαδοχικά
, για κάποια σταθερά
(Λόγω πυκνότητας του
στο
.)
Τελικά

 .
. έχουμε
έχουμε  ή
ή  .
.Τυπογραφικό ήταν. Συγνώμη για τη σύγχυση.Ανδρέας Πούλος έγραψε: ↑Δευ Νοέμ 07, 2022 11:26 pmΑγαπητέ Γιώργο, δεν βρήκα τρόπο για προσωπική επικοινωνία για διόρθωση του τυπογραφικού σου λάθους,
γι΄ αυτό στέλνω δημόσιο μήνυμα.
Γράφεις
(g(x)+2)(g(y)+2)-6=3g(x+y) ισοδύναμα f(x)f(y)=f(x+y),
όπου.
Εξάλλου, εύκολα διαπιστώνουμε ότι γιαέχουμε
ή
.
Αυτό το δεδομένο αντιφάσκει με την προτεινόμενη λύση σου.
Εν τέλειthepigod762 έγραψε: ↑Δευ Νοέμ 07, 2022 10:33 pmΓράφουμε
όπου
Σαφώς,
και γιαγια κάποιο
που ικανοποιεί.
Γιατώρα παίρνουμε λογάριθμο και στα δύο μέλη που δίνει
οπότε ηικανοποιεί Cauchy, και επειδή είναι μονότονη έχουμε διαδοχικά
, για κάποια σταθερά
(Λόγω πυκνότητας του
στο
.)
Τελικά

 , όπου
, όπου 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης