![f:\mathbb{Q}[x]\to \mathbb{Q}[x] f:\mathbb{Q}[x]\to \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/259001dd8722318ffda0e614643db3af.png) που είναι τέτοια ώστε
που είναι τέτοια ώστε για κάθε
![P,Q \in \mathbb{Q}[x] P,Q \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/2cc874c041e23cd67daf552fdba615ee.png) να ισχύουν
να ισχύουν![Q[x] Q[x]](/forum/ext/geomar/texintegr/latexrender/pictures/d3dfdf7d34899bdc6fe14638f21a7cd4.png) το σύνολο των πολυωνύμων με ρητούς συντελεστές.
το σύνολο των πολυωνύμων με ρητούς συντελεστές.Συντονιστές: achilleas, emouroukos, silouan
![f:\mathbb{Q}[x]\to \mathbb{Q}[x] f:\mathbb{Q}[x]\to \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/259001dd8722318ffda0e614643db3af.png) που είναι τέτοια ώστε
που είναι τέτοια ώστε ![P,Q \in \mathbb{Q}[x] P,Q \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/2cc874c041e23cd67daf552fdba615ee.png) να ισχύουν
να ισχύουν

![Q[x] Q[x]](/forum/ext/geomar/texintegr/latexrender/pictures/d3dfdf7d34899bdc6fe14638f21a7cd4.png) το σύνολο των πολυωνύμων με ρητούς συντελεστές.
το σύνολο των πολυωνύμων με ρητούς συντελεστές.Παρατηρώ ότι ηΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑Σάβ Σεπ 24, 2022 4:59 pmΝα βρεθούν όλες οι συναρτήσειςπου είναι τέτοια ώστε
για κάθενα ισχύουν
το σύνολο των πολυωνύμων με ρητούς συντελεστές.
![f(P)=0 , \forall P\in\mathbb{Q}[x] f(P)=0 , \forall P\in\mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/1d60371204c205ea21af040087d73e4a.png) είναι λύση, οπότε στο εξής θεωρώ ότι η
είναι λύση, οπότε στο εξής θεωρώ ότι η  δεν είναι η μηδενική.
δεν είναι η μηδενική. , στην
, στην  :
:  .
. , όπου
, όπου  τυχών ρητός στην
τυχών ρητός στην  :
:  , δηλαδή τα σταθερά πολυώνυμα απεικονίζονται μέσω της
, δηλαδή τα σταθερά πολυώνυμα απεικονίζονται μέσω της  στο μηδενικό πολυώνυμο.
στο μηδενικό πολυώνυμο. , είναι
, είναι  οπότε στην
οπότε στην  :
: ![f(P)=f(P)f(X) \implies f(P)(1-f(X))=0 , \forall P\in\mathbb{Q}[x] f(P)=f(P)f(X) \implies f(P)(1-f(X))=0 , \forall P\in\mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/aee7c71b32d14ed65971afe2193416f3.png) .
.![\exists P\in\mathbb{Q}[x] \exists P\in\mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/4b6cb5431b597c7d69b500a043789794.png) με
με  . Βάζοντας αυτό στην πάνω παίρνω
. Βάζοντας αυτό στην πάνω παίρνω  .
. , βάζω
, βάζω  (σταθερό) στην
(σταθερό) στην  :
: ![f(qP)=qf(P) , \forall q\in\mathbb{Q} , \forallP\in\mathbb{Q}[x] \text{ }(4) f(qP)=qf(P) , \forall q\in\mathbb{Q} , \forallP\in\mathbb{Q}[x] \text{ }(4)](/forum/ext/geomar/texintegr/latexrender/pictures/3444e3bde80afae221519157e84ce0eb.png) .
. .
. , έχω το
, έχω το  .
. έχω
έχω  , τότε:
, τότε: .
. .
. έχω:
έχω:  .
. . Βάζω στη
. Βάζω στη 
 . Τότε:
. Τότε: .
. μη-μηδενικό σταθερό για κάθε
μη-μηδενικό σταθερό για κάθε  . Μπορώ λοιπόν να ορίσω
. Μπορώ λοιπόν να ορίσω  με τύπο:
με τύπο: .
. για
για 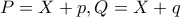 παίρνω:
παίρνω: .
. ,όπου
,όπου  .
. (γιατί;).
(γιατί;). . Στην
. Στην  βάζοντας
βάζοντας  :
:![f(Q+q)=f(Q) , \forall Q \in\mathbb{Q}[x]\text{ } (6) f(Q+q)=f(Q) , \forall Q \in\mathbb{Q}[x]\text{ } (6)](/forum/ext/geomar/texintegr/latexrender/pictures/da8667dd0e545bb1598c7ab6257d9deb.png) .
.![P=a_0+a_1X+\dots +a_nX^n \in\mathbb{Q}[x] P=a_0+a_1X+\dots +a_nX^n \in\mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/21f088d01e562865c0b7b9d9dbbdb3ff.png) ισχύει
ισχύει  .
. .
. , τότε
, τότε 
 ο ισχυρισμός είναι αληθής.
ο ισχυρισμός είναι αληθής. :
:  . Τότε:
. Τότε: 
 .
. για κάθε πολυώνυμο
για κάθε πολυώνυμο  .
. που βρήκαμε ικανοποιεί τις
που βρήκαμε ικανοποιεί τις  (γνωστές ιδιότητες της παραγώγου), οπότε
(γνωστές ιδιότητες της παραγώγου), οπότεΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες