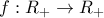 τέτοιες ώστε για κάθε
τέτοιες ώστε για κάθε  θετικούς πραγματικούς να ισχύει
θετικούς πραγματικούς να ισχύει 
Συντονιστές: achilleas, emouroukos, silouan
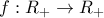 τέτοιες ώστε για κάθε
τέτοιες ώστε για κάθε  θετικούς πραγματικούς να ισχύει
θετικούς πραγματικούς να ισχύει 
 η οποία ικανοποιεί τη σχέση
η οποία ικανοποιεί τη σχέση
 .
. . Για
. Για  και
και  στην πιο πάνω σχέση παίρνουμε
στην πιο πάνω σχέση παίρνουμε  που μας δείχνει ότι η
που μας δείχνει ότι η  είναι επί.
είναι επί. ώστε
ώστε  . Για
. Για  παίρνουμε
παίρνουμε  , άρα
, άρα 
 . Για
. Για  παίρνουμε
παίρνουμε  ενώ για
ενώ για  παίρνουμε
παίρνουμε  . Από αυτά τα δύο έχουμε
. Από αυτά τα δύο έχουμε
 . Από το πιο πάνω είναι άμεσο ότι η
. Από το πιο πάνω είναι άμεσο ότι η  είναι 1-1. Αφού λοιπόν έχουμε και
είναι 1-1. Αφού λοιπόν έχουμε και  για κάθε
για κάθε  τότε παίρνουμε ότι
τότε παίρνουμε ότι  για κάθε
για κάθε  .
. για κάθε
για κάθε  η οποία προφανώς ικανοποιεί τη συνθήκη.
η οποία προφανώς ικανοποιεί τη συνθήκη.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης