Αριθμός δυνατών τιμών όρου ακολουθίας

#1

Έστω μια ακολουθία (a_n)

θετικών αριθμών με a_1=1

και

$\displaystyle a_{n+1}+a_n=\left(a_{n+1}-a_n\right)^2,$

για κάθε $n\geq 1$ . Να προσδιορισθεί το πλήθος των δυνατών τιμών του $a_{2021}$ .

Φιλικά,

Αχιλλέας

#2

achilleas έγραψε: ↑
Τετ Μαρ 09, 2022 8:24 pm
Έστω μια ακολουθία θετικών αριθμών με και

$\displaystyle a_{n+1}+a_n=\left(a_{n+1}-a_n\right)^2,$

για κάθε $n\geq 1$ . Να προσδιορισθεί το πλήθος των δυνατών τιμών του $a_{2021}$ .

Απάντηση: Γενικότερα, για $n\ge 2$ οι τιμές του a_n

είναι οι αριθμοί $\dfrac {1}{2}k(k+1)$ όπου (τους γράφω ανάποδα) $k=n,\, n-2, n-4,\, ...$

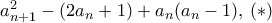Πράγματι, η δοθείσα γράφεται $a_{n+1}^2-(2a_n+1) + a_n(a_n-1),\,(*)$ . Άρα εύκολα βρίσκουμε ότι το a_2

είναι

ή

αλλά κραατάμε μόνο το θετικό. Πίσω στην (*)

βρίσκουμε

ίσον

ή

. Όμοια

ίσον

ή

(όπως περιγράψαμε).

Για το επαγωγικό βήμα έχουμε για κάποιο

ως άνω ότι $a_n= \dfrac {1}{2}k(k+1)$ , άρα η (*)

δίνει

$a_{n+1}^2-[k(k+1)+1]a_{n+1} +\dfrac {1}{2}k(k+1)\left (\dfrac {1}{2}k(k+1)-1 \right )$ , ισόδύναμα

$a_{n+1}^2-[k^2+k+1]a_{n+1} +\dfrac {1}{4}(k^2+k)(k^2+k-2)$ .

Oι ρίζες του τελευταίου είναι οι $a_{n+1}= \dfrac {1}{2} (k+1)(k+2)$ και $a_{n+1}=\dfrac {1}{2}(k-1)k$ (δηλαδή ο επόμενος και ένας πίσω), από όπου εύκολα ολοκληρώνεται η επαγωγή.

Edit: Έκανα μικρή διόρθωση.

Αριθμός δυνατών τιμών όρου ακολουθίας

Αριθμός δυνατών τιμών όρου ακολουθίας

Re: Αριθμός δυνατών τιμών όρου ακολουθίας

Μέλη σε σύνδεση