 θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
θετικοί πραγματικοί αριθμοί τέτοιοι ώστε  . Να δειχθεί ότι
. Να δειχθεί ότι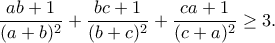
Φιλικά,
Αχιλλέας
Συντονιστές: achilleas, emouroukos, silouan
Μη αναγνωσμένη δημοσίευση από achilleas » Σάβ Ιαν 29, 2022 1:46 pm
 θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
θετικοί πραγματικοί αριθμοί τέτοιοι ώστε  . Να δειχθεί ότι
. Να δειχθεί ότι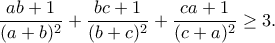
Μη αναγνωσμένη δημοσίευση από matha » Σάβ Ιαν 29, 2022 2:01 pm
 , οπότε η συνθήκη γράφεται
, οπότε η συνθήκη γράφεται 


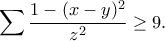

 ή
ή 
Επιστροφή σε “Άλγεβρα - Επίπεδο Αρχιμήδη (Seniors)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off