 και
και  να δείξετε ότι
να δείξετε ότι ![\dfrac{a}{\sqrt[3]{a+2b}}+\dfrac{b}{\sqrt[3]{b+2c}}+\dfrac{c}{\sqrt[3]{c+2a}} \geq 1 \dfrac{a}{\sqrt[3]{a+2b}}+\dfrac{b}{\sqrt[3]{b+2c}}+\dfrac{c}{\sqrt[3]{c+2a}} \geq 1](/forum/ext/geomar/texintegr/latexrender/pictures/2a88a64cfd42af7b46e8aab0db2dc7f4.png)
Συντονιστές: achilleas, emouroukos, silouan
 και
και  να δείξετε ότι
να δείξετε ότι ![\dfrac{a}{\sqrt[3]{a+2b}}+\dfrac{b}{\sqrt[3]{b+2c}}+\dfrac{c}{\sqrt[3]{c+2a}} \geq 1 \dfrac{a}{\sqrt[3]{a+2b}}+\dfrac{b}{\sqrt[3]{b+2c}}+\dfrac{c}{\sqrt[3]{c+2a}} \geq 1](/forum/ext/geomar/texintegr/latexrender/pictures/2a88a64cfd42af7b46e8aab0db2dc7f4.png)
Σωστά, (έχω και εγώ μια ελαφρώς διαφορετική λύση), απλά καλό θα ήταν για να γίνεται κατανοητή η λύση από όλα τα μέλη του
![\displaystyle{(a+2b)+1+1\geq 3\sqrt[3]{a+2b}\implies a+2b+2\geq 3\sqrt[3]{a+2b}.} \displaystyle{(a+2b)+1+1\geq 3\sqrt[3]{a+2b}\implies a+2b+2\geq 3\sqrt[3]{a+2b}.}](/forum/ext/geomar/texintegr/latexrender/pictures/8f7dfb90b1ac3a509630141ea18365fd.png)
![\displaystyle{\sum \frac{a}{\sqrt[3]{a+2b}}\geq 3\sum \frac{a}{a+2b+2}.} \displaystyle{\sum \frac{a}{\sqrt[3]{a+2b}}\geq 3\sum \frac{a}{a+2b+2}.}](/forum/ext/geomar/texintegr/latexrender/pictures/7881c95f0447aab50cceef2457597a53.png)
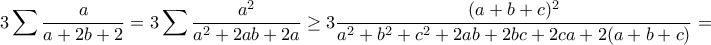

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες