 τέτοια ώστε να ισχύει η σχέση
τέτοια ώστε να ισχύει η σχέση για κάθε
για κάθε  .
.
Συντονιστές: achilleas, emouroukos, silouan
 τέτοια ώστε να ισχύει η σχέση
τέτοια ώστε να ισχύει η σχέση για κάθε
για κάθε  .
.
 παίρνω
παίρνω  .
. παίρνω
παίρνω  για κάθε
για κάθε  . Αφού αυτό ισχύει για άπειρες τιμές του
. Αφού αυτό ισχύει για άπειρες τιμές του  τότε
τότε  για κάποιο πολυώνυμο δύο μεταβλητών
για κάποιο πολυώνυμο δύο μεταβλητών  .
.  για κάθε
για κάθε  .
. παίρνω
παίρνω  για κάθε
για κάθε  άρα
άρα 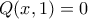 για κάθε
για κάθε  . Όπως πριν παίρνω
. Όπως πριν παίρνω  που δίνει
που δίνει  για κάθε
για κάθε  . Τότε ισχύει επίσης ότι
. Τότε ισχύει επίσης ότι  για κάθε
για κάθε  άρα και για κάθε
άρα και για κάθε  .
. παίρνω
παίρνω  που όπως πριν μου δίνει
που όπως πριν μου δίνει  . Με παρόμοιο τρόπο όπως προηγουμένως καταλήγω σε
. Με παρόμοιο τρόπο όπως προηγουμένως καταλήγω σε  για κάθε
για κάθε  . Όμως το
. Όμως το  έχει μικρότερο βαθμό από το
έχει μικρότερο βαθμό από το  . Αυτή η διαδικασία δεν μπορεί να συνεχίζεται επ' άπειρον. Άρα πρέπει η
. Αυτή η διαδικασία δεν μπορεί να συνεχίζεται επ' άπειρον. Άρα πρέπει η  να είναι ταυτοτικά
να είναι ταυτοτικά  .
. και έστω ότι υπάρχουν άπειρα σύνολα
και έστω ότι υπάρχουν άπειρα σύνολα  ώστε
ώστε  για κάθε
για κάθε  . Τότε
. Τότε  για κάθε
για κάθε  .
. . Η περίπτωση
. Η περίπτωση  είναι αρκετά γνωστή. Γράφουμε τώρα
είναι αρκετά γνωστή. Γράφουμε τώρα 
 .
.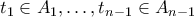 . Ως πολυώνυμο μίας μεταβλητής το
. Ως πολυώνυμο μίας μεταβλητής το  μηδενίζεται σε άπειρες τιμές του
μηδενίζεται σε άπειρες τιμές του  . Αυτό σημαίνει πως είναι το μηδενικό πολυώνυμο. Άρα
. Αυτό σημαίνει πως είναι το μηδενικό πολυώνυμο. Άρα  .
.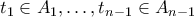 . Άρα από την επαγωγική υπόθεση τα
. Άρα από την επαγωγική υπόθεση τα  είναι μηδενικά πολυώνυμα και άρα το ίδιο ισχύει και για το
είναι μηδενικά πολυώνυμα και άρα το ίδιο ισχύει και για το  .
.
 . Γνωρίζοντας ότι ισούται με
. Γνωρίζοντας ότι ισούται με  για κάθε
για κάθε  παίρνω ότι ισούται με
παίρνω ότι ισούται με  για κάθε
για κάθε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης