
και

όπου
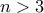 φυσικός.
φυσικός.1)Βρείτε τα
 για τα οποία το
για τα οποία το  διαιρεί το
διαιρεί το 
2)Για
 βρείτε το πηλίκο της διαίρεσης
βρείτε το πηλίκο της διαίρεσηςΣυντονιστές: achilleas, emouroukos, silouan


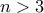 φυσικός.
φυσικός. για τα οποία το
για τα οποία το  διαιρεί το
διαιρεί το 
 βρείτε το πηλίκο της διαίρεσης
βρείτε το πηλίκο της διαίρεσηςΑς την δυσκολέψουμε (*) λίγο: Από ταΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Αύγ 12, 2020 10:02 pmΘεωρούμε τα πολυώνυμα
και
όπουφυσικός.
1)Βρείτε ταγια τα οποία το
διαιρεί το
2)Γιαβρείτε το πηλίκο της διαίρεσης
 που θα βρείτε ποια είναι εκείνα για τα οποία το
που θα βρείτε ποια είναι εκείνα για τα οποία το  διαιρείται από το
διαιρείται από το  ;
; .
.1)ΕίναιΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Αύγ 12, 2020 10:02 pmΘεωρούμε τα πολυώνυμα
και
όπουφυσικός.
1)Βρείτε ταγια τα οποία το
διαιρεί το
2)Γιαβρείτε το πηλίκο της διαίρεσης
 (απλό).
(απλό). με
με 
 .
. .Αν
.Αν  τότε
τότε  το οποίο εύκολα προκύπτει αδύνατο αφού
το οποίο εύκολα προκύπτει αδύνατο αφού 
 περιττός και πρέπει
περιττός και πρέπει 
 πρέπει
πρέπει 

 αυτό ισχύει(ελπίζω να έκανα σωστά τις πράξεις),οπότε ικανή και αναγκαία συνθήκη είναι
αυτό ισχύει(ελπίζω να έκανα σωστά τις πράξεις),οπότε ικανή και αναγκαία συνθήκη είναι  .
. )
)

 θα είναι συμμετρικό πολυώνυμο ως προς τα
θα είναι συμμετρικό πολυώνυμο ως προς τα  3ου βαθμου της μορφής
3ου βαθμου της μορφής 
 παίρνουμε
παίρνουμε 
 παίρνουμε
παίρνουμε 
 και επαληθεύουμε ότι όντως ισχύει.
και επαληθεύουμε ότι όντως ισχύει.Ίσως να μην ισχύουν τα παρακάτω..συγχωρέστε μεMihalis_Lambrou έγραψε: ↑Πέμ Αύγ 13, 2020 12:12 amΑς την δυσκολέψουμε (*) λίγο: Από ταΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Αύγ 12, 2020 10:02 pmΘεωρούμε τα πολυώνυμα
και
όπουφυσικός.
1)Βρείτε ταγια τα οποία το
διαιρεί το
2)Γιαβρείτε το πηλίκο της διαίρεσης
που θα βρείτε ποια είναι εκείνα για τα οποία το
διαιρείται από το
;
(*) Στην πραγματικότητα δεν πρόκειται για δυσκολότερη άσκηση: Λύνοντας την αρχική άσκηση του Σταύρου, μία λίγο πιο προσεκτική μελέτη δίνει και αυτό που ζητώ. Έμμεσα το είπε και ο Σταύρος όταν ζήτησε το πηλίκο στην περίπτωση.
 ως προς
ως προς  προκύπτει η
προκύπτει η  .
.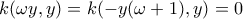 (αυτό το ξέρω για συνάρτηση μίας μεταβλητής,δουλεύει και εδώ όμως σωστά;)
(αυτό το ξέρω για συνάρτηση μίας μεταβλητής,δουλεύει και εδώ όμως σωστά;)


 .
. είναι δεκτή τιμή οπότε συμπλήρωσα στην λύση μου στο τέλος την παραγοντοποίηση του
είναι δεκτή τιμή οπότε συμπλήρωσα στην λύση μου στο τέλος την παραγοντοποίηση του  να φαίνεται.
να φαίνεται. μεταβλητών τότε μπορούμε
μεταβλητών τότε μπορούμε  μεταβλητών.
μεταβλητών.



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες