
και

1)Δείξτε ότι το
 διαιρεί το πολυώνυμο
διαιρεί το πολυώνυμο 
όταν το
 περιττός αριθμός
περιττός αριθμός2)Βρείτε για ποια
 το
το  διαιρεί το
διαιρεί το 
Συντονιστές: achilleas, emouroukos, silouan


 διαιρεί το πολυώνυμο
διαιρεί το πολυώνυμο 
 περιττός αριθμός
περιττός αριθμός το
το  διαιρεί το
διαιρεί το 
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Αύγ 09, 2020 9:40 pmΘωρούμε τα πολυώνυμα
και
1)Δείξτε ότι τοδιαιρεί το πολυώνυμο
όταν τοπεριττός αριθμός
 περιττός το
περιττός το  μηδενίζεται όταν
μηδενίζεται όταν  (άμεσο). Άρα, κοιτώντας το ως πολυώνυμο του
(άμεσο). Άρα, κοιτώντας το ως πολυώνυμο του  , είναι
, είναι  για κάποιο πολυώνυμο
για κάποιο πολυώνυμο  .
.  μηδενίζεται όταν
μηδενίζεται όταν 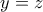 , σημαίνει ότι ισχύει το ίδιο για το ίσο του
, σημαίνει ότι ισχύει το ίδιο για το ίσο του  , και άρα μηδενίζεται το
, και άρα μηδενίζεται το  . Έπεται ότι
. Έπεται ότι  για κάποιο πολυώνυμο
για κάποιο πολυώνυμο  , δηλαδή
, δηλαδή  .
. . Καταλήγουμε ότι
. Καταλήγουμε ότι  .
.
 όπου
όπου  . (Ο έλεγχος είναι απλός χρησιμοποιώντας το
. (Ο έλεγχος είναι απλός χρησιμοποιώντας το  καθώς και το
καθώς και το  .)
.) . Παρατηρούμε ότι
. Παρατηρούμε ότι ![f_n(-\omega y-\omega^2 z,y,z) = (y-z)^n[\omega^{2n}+1+\omega^n] f_n(-\omega y-\omega^2 z,y,z) = (y-z)^n[\omega^{2n}+1+\omega^n]](/forum/ext/geomar/texintegr/latexrender/pictures/8c03ce5d9a2e6cf832ea9f70c29c53f2.png) . Επίσης έχουμε και
. Επίσης έχουμε και ![f_n(-\omega^2 y - \omega z,y,z)=(y-z)^n[\omega^n + 1 + \omega^{2n}] f_n(-\omega^2 y - \omega z,y,z)=(y-z)^n[\omega^n + 1 + \omega^{2n}]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb052cbb324d554f21b6953f5a39929.png)
 (απλό) με τον ίδιο τρόπο που εξήγησε αρκετά αναλυτικά ο Μιχάλης καταλήγουμε ότι το
(απλό) με τον ίδιο τρόπο που εξήγησε αρκετά αναλυτικά ο Μιχάλης καταλήγουμε ότι το  διαιρεί το
διαιρεί το  αν και μόνο αν
αν και μόνο αν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: MSN [Bot] και 1 επισκέπτης