Έστω
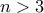 ένας θετικός ακέραιος, και
ένας θετικός ακέραιος, και  που ικανοποιούν τις επόμενες ιδιότητες:
που ικανοποιούν τις επόμενες ιδιότητες:α)

 , και
, καιβ) ο αριθμός των τρόπων που μπορούμε να επιλέξουμε
 ώστε
ώστε  είναι μεγαλύτερος ή ίσος του
είναι μεγαλύτερος ή ίσος του  .
.Να βρείτε, συναρτήσει του
 , την μέγιστη τιμή που μπορεί να πάρει ο λόγος:
, την μέγιστη τιμή που μπορεί να πάρει ο λόγος:  .
.
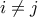 έχουμε
έχουμε  Επομένως είτε
Επομένως είτε  , είτε
, είτε  .
. , τότε για κάθε
, τότε για κάθε  έχουμε
έχουμε  ή
ή  . Μπορούμε λοιπόν να υποθέσουμε ότι
. Μπορούμε λοιπόν να υποθέσουμε ότι  από τους αριθμούς είναι ίσοι με
από τους αριθμούς είναι ίσοι με  και οι άλλοι
και οι άλλοι  είναι ίσοι με
είναι ίσοι με  . Η συνθήκη (β) μας λέει ότι
. Η συνθήκη (β) μας λέει ότι  . Αναγκαστικά λοιπόν πρέπει
. Αναγκαστικά λοιπόν πρέπει  . (Μπορεί να δειχθεί ότι
. (Μπορεί να δειχθεί ότι  αλλά δεν θα το χρησιμοποιήσουμε.)
αλλά δεν θα το χρησιμοποιήσουμε.)
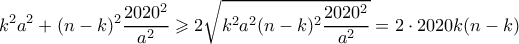
 λαμβάνεται όταν έχουμε και ισότητα στην Cauchy-Schwarz. Δηλαδή όταν
λαμβάνεται όταν έχουμε και ισότητα στην Cauchy-Schwarz. Δηλαδή όταν 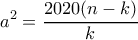
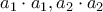 ...)
...)