 του σχήματος το
του σχήματος το  είναι ύψος και οι γωνίες
είναι ύψος και οι γωνίες  είναι γνωστές και οξείες. Επί των πλευρών
είναι γνωστές και οξείες. Επί των πλευρών  θεωρούμε τα σημεία
θεωρούμε τα σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  Να βρείτε συναρτήσει των
Να βρείτε συναρτήσει των 
την τιμή της
 για την οποία μεγιστοποιείται το εμβαδόν του τριγώνου
για την οποία μεγιστοποιείται το εμβαδόν του τριγώνου 
Συντονιστές: achilleas, emouroukos, silouan
 του σχήματος το
του σχήματος το  είναι ύψος και οι γωνίες
είναι ύψος και οι γωνίες  είναι γνωστές και οξείες. Επί των πλευρών
είναι γνωστές και οξείες. Επί των πλευρών  θεωρούμε τα σημεία
θεωρούμε τα σημεία  αντίστοιχα, ώστε
αντίστοιχα, ώστε  Να βρείτε συναρτήσει των
Να βρείτε συναρτήσει των 
 για την οποία μεγιστοποιείται το εμβαδόν του τριγώνου
για την οποία μεγιστοποιείται το εμβαδόν του τριγώνου 

Η σχέση επαληθεύεται σε γεωμετρική κατασκευή που έκανα ( χωρίς να γνωρίζω αυτή τη τριγωνομετρική σχέση ) γιατί η
 διέρχεται από "σταθερό" σημείο , συγκεκριμένα από το συζυγές αρμονικό του
διέρχεται από "σταθερό" σημείο , συγκεκριμένα από το συζυγές αρμονικό του  . ως προς τα
. ως προς τα 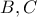 .
. οι προβολές των
οι προβολές των  στην
στην  και
και  η τομή των
η τομή των  .
. . Θέτω :
. Θέτω :  .
. και
και 
 και ομοίως:
και ομοίως:  .
. 
 και αφού :
και αφού : 

 ,έστω
,έστω  και λόγω των
και λόγω των  είναι:
είναι: 
 :
: .
.  παρουσιάζει μέγιστο
παρουσιάζει μέγιστο 
 Κατασκευή: Το ύψος
Κατασκευή: Το ύψος  τέμνει τον περιγεγραμμένο κύκλο στο
τέμνει τον περιγεγραμμένο κύκλο στο  και ο κύκλος διαμέτρου
και ο κύκλος διαμέτρου  την
την 
 H παράλληλη από το
H παράλληλη από το  στην
στην  τέμνει την
τέμνει την  στο ζητούμενο σημείο
στο ζητούμενο σημείο 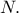 Τα υπόλοιπα είναι απλά.
Τα υπόλοιπα είναι απλά. Από κατασκευής είναι
Από κατασκευής είναι  και
και
 αν
αν  θα έχω:
θα έχω:  . έτσι :
. έτσι : 


 έχω:
έχω:  και η
και η  δίδει :
δίδει :  .
. εσωτερικά σε λόγο:
εσωτερικά σε λόγο:  . Φέρνω στο
. Φέρνω στο  κάθετη επί την
κάθετη επί την  και τέμνει την
και τέμνει την  στο
στο 
 .
. τέμνει τη
τέμνει τη  στο
στο  η δέσμη :
η δέσμη :  είναι
είναι  είναι αρμονική
είναι αρμονική να το ενώσω με το
να το ενώσω με το  και να προκύψει έτσι το
και να προκύψει έτσι το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες